题目内容
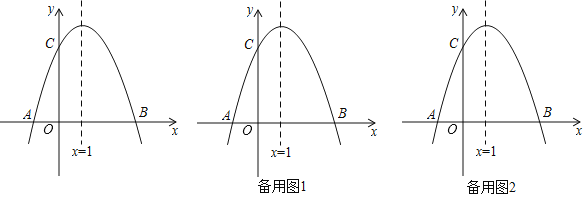
【题目】已知关于x的二次函数y=ax2﹣4ax+a+1(a>0)
(1)若二次函数的图象与x轴有交点,求a的取值范围;
(2)若P(m,n)和Q(5,b)是抛物线上两点,且n>b,求实数m的取值范围;
(3)当m≤x≤m+2时,求y的最小值(用含a、m的代数式表示).
【答案】(1)a≥![]() ;(2)m<﹣1或m>5;(3)y的最小值为:am2﹣3a+1或﹣3a+1或am2﹣4am+a+1.
;(2)m<﹣1或m>5;(3)y的最小值为:am2﹣3a+1或﹣3a+1或am2﹣4am+a+1.
【解析】
(1)令对应一元二次方程根的判别式大于等于0,然后解答即可;
(2)根据抛物线的对称轴为直线x=![]() ,当n=b时,根据函数的对称性,可得m=-1,最后确定m的取值范围即可;
,当n=b时,根据函数的对称性,可得m=-1,最后确定m的取值范围即可;
(3)分m<0,0≤m≤2,m>2三种情况别求解即可.
解:(1)由题意得:
△=(﹣4a)2﹣4a(a+1)≥0,且a>0,
解得:a≥![]() ;
;
(2)抛物线的对称轴为直线x=﹣![]() =2,
=2,
当n=b时,根据函数的对称性,则m=﹣1或m=5,
故实数m的取值范围为:m<﹣1或m>5;
(3)①当m+2<2时,即m<0时,
函数在x=m+2时,取得最小值,
ymin=a(m+2)2﹣4a(m+2)+a+1=am2﹣3a+1;
②当m≤2≤m+2时,即0≤m≤2,
函数在顶点处取得最小值,
即ymin=4a﹣4a×2+a+1=﹣3a+1;
③当m>2时,
函数在x=m时,取得最小值,
ymin=am2﹣4am+a+1;
综上,y的最小值为:am2﹣3a+1或﹣3a+1或am2﹣4am+a+1.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目