题目内容
【题目】在探究三角形内角和等于180°的证明过程时，小明同学通过认真思考后认为，可以通过剪拼的方法将一个角剪下来，然后把这个角进行平移，从而实现把三角形的三个内角转移到一个平角中去，如图所示：
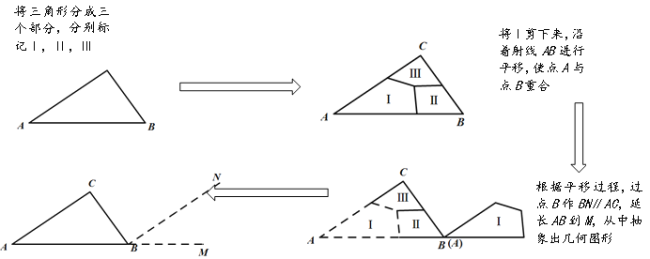
（1）小明同学根据剪拼的过程，抽象出几何图形；并进行了推理证明，请你帮助小明完成
证明过程．
证明：过点B作BN//AC,延长AB到M
∵
∴
∵
∴
（2）小军仿照小明的方法将三角形的三个内角都进行了移动，也将三个内角转移到一个平 角中去，只不过平角的顶点放到了AB边上，如图所示：请你仿照小明的证明过程，抽象出几何图形再进行证明．
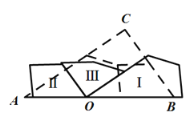
（3）小兰的方法和小明以及小军的方法都不相同，她将三角形三个内角分别沿某一条直线翻折，一共进行了三次尝试，如图所示：
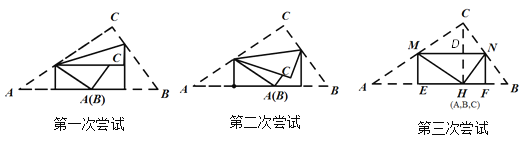
小兰第三次成功的关键是什么，请你写出证明思路．
【答案】（1）见解析；（2）见解析；（3）见解析.
【解析】
（1）根据平行线的性质即可作答；
（2）根据平行线的性质结合平角的性质即可证明；
（3）根据垂直的定义以及翻折的性质得
，
，
，从而证得结论.
(1)两直线平行，同位角相等； 两直线平行，内错角相等．
(2)
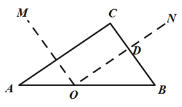
证明：Ｏ是线段AB上的一点，过点Ｏ作ON∥AC 交BC于点D， 过点Ｏ作OM∥BC，
∵
∴
∵
∴
∵
∴
．
(3)关键：将
沿点C所在的垂直于AB的直线翻折，折痕与AB的交点为H，使点C与点H重合，确定折痕MN，将
沿点M所在的垂直于AB的直线翻折，折痕与AB的交点为E ，将
沿点N所在的垂直于AB的直线翻折，折痕与AB的交点为F
证明思路：根据翻折的性质知：
,
，MN是CH的垂直平分线，
∴
,
,
∴
∴
同理
∴，
∵
∴．
练习册系列答案
阅读快车系列答案
相关题目
