题目内容
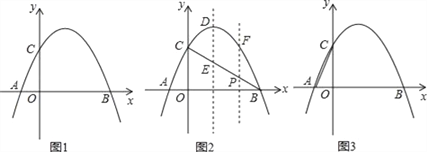
【题目】如图1,抛物线y=﹣x2+2x+3与x轴相交于A、B两点(点A在点B的左侧),与y轴相交于点C.
(1)直接写出A、B、C三点的坐标和抛物线的对称轴;
(2)如图2,连接BC,与抛物线的对称轴交于点E,点P为线段BC上的一个动点,过点P作PF∥DE交抛物线于点F,设点P的横坐标为m;用含m的代数式表示线段PF的长;并求出当m为何值时,四边形PEDF为平行四边形?
(3)如图3,连接AC,在x轴上是否存在点Q,使△ACQ为等腰三角形,若存在,请求出点Q的坐标,若不存在,请说明理由.
【答案】(1)A(﹣1,0),B(3,0),C(0,3).对称轴是直线x=1;(2)PF=﹣m2+3m.当m=2时,四边形PEDF为平行四边形;(3)存在,Q1(4,0),Q2(1,0),Q3(![]() ﹣1,0),Q4(﹣
﹣1,0),Q4(﹣![]() ﹣1,0).
﹣1,0).
【解析】试题分析:(1)通过解方程﹣x2+2x+3=0可得A点和B点坐标,再计算自变量为0时的函数值可得到C点坐标,然后利用对称性可确定抛物线的对称轴;(2)先利用待定系数法求出直线BC的函数关系式为y=﹣x+3,再确定E,D点坐标,E(1,2),D(1,4),表示出P(m,﹣m+3),F(m,﹣m2+2m+3),两点纵坐标相减便得PF=﹣m2+3m,接着计算出DE=2,然后利用平行四边形的判定方法,即一组对边平行且相等的四边形是平行四边形,得到﹣m2+3m=2,再解方程求出m即可.(3)分三种情况:QA=QC;CA=CQ;AC=AQ;进行讨论即可求解.
试题解析:(1)当y=0时,﹣x2+2x+3=0,即-(x-3)(x+1)=0,解得x1=﹣1,x2=3,则A(﹣1,0),B(3,0),当x=0时,y=﹣x2+2x+3=3,则C(0,3);利用A,B点坐标求出抛物线的对称轴是直线x=![]() =1;所以A(﹣1,0),B(3,0),C(0,3).对称轴是直线x=1;(2)设直线BC的函数关系式为y=kx+b,把B(3,0),C(0,3)分别代入得
=1;所以A(﹣1,0),B(3,0),C(0,3).对称轴是直线x=1;(2)设直线BC的函数关系式为y=kx+b,把B(3,0),C(0,3)分别代入得![]() ,解得k=﹣1,b=3,∴直线BC的函数关系式为y=﹣x+3,∵对称轴是直线x=1,∴E(1,2),∵y=﹣x2+2x+3=﹣(x﹣1)2+4,∴顶点D的坐标为(1,4),当x="m" 时,y=﹣m+3,∴P(m,﹣m+3),F(m,﹣m2+2m+3),∴线段PF=﹣m2+2m+3﹣(﹣m+3)=﹣m2+3m,即线段PF=﹣m2+3m,又线段DE=4﹣2=2,∵PF∥DE,∴当PF=ED时,四边形PEDF为平行四边形,即﹣m2+3m=2,解得m1=2,m2=1(不合题意,舍去),∴当m=2时,四边形PEDF为平行四边形;(3)分三种情况:QA=QC;CA=CQ;AC=AQ;进行讨论:设在x轴上存在点Q(x,0),使△ACQ为等腰三角形.分三种情况:①如果QA=QC,那么(x+1)2=x2+32,解得x=4,则点Q1(4,0);②如果CA=CQ,那么12+32=x2+32,解得x1=1,x2=﹣1(不合题意舍去),则点Q2(1,0);③如果AC=AQ,那么12+32=(x+1)2,解得x1=
,解得k=﹣1,b=3,∴直线BC的函数关系式为y=﹣x+3,∵对称轴是直线x=1,∴E(1,2),∵y=﹣x2+2x+3=﹣(x﹣1)2+4,∴顶点D的坐标为(1,4),当x="m" 时,y=﹣m+3,∴P(m,﹣m+3),F(m,﹣m2+2m+3),∴线段PF=﹣m2+2m+3﹣(﹣m+3)=﹣m2+3m,即线段PF=﹣m2+3m,又线段DE=4﹣2=2,∵PF∥DE,∴当PF=ED时,四边形PEDF为平行四边形,即﹣m2+3m=2,解得m1=2,m2=1(不合题意,舍去),∴当m=2时,四边形PEDF为平行四边形;(3)分三种情况:QA=QC;CA=CQ;AC=AQ;进行讨论:设在x轴上存在点Q(x,0),使△ACQ为等腰三角形.分三种情况:①如果QA=QC,那么(x+1)2=x2+32,解得x=4,则点Q1(4,0);②如果CA=CQ,那么12+32=x2+32,解得x1=1,x2=﹣1(不合题意舍去),则点Q2(1,0);③如果AC=AQ,那么12+32=(x+1)2,解得x1=![]() ﹣1,x2=﹣
﹣1,x2=﹣![]() ﹣1,则点Q3(
﹣1,则点Q3(![]() ﹣1,0),Q4(﹣
﹣1,0),Q4(﹣![]() ﹣1,0);综上所述存在点Q,使△ACQ为等腰三角形.它的坐标为:Q1(4,0),Q2(1,0),Q3(
﹣1,0);综上所述存在点Q,使△ACQ为等腰三角形.它的坐标为:Q1(4,0),Q2(1,0),Q3(![]() ﹣1,0),Q4(﹣
﹣1,0),Q4(﹣![]() ﹣1,0).
﹣1,0).

 阅读快车系列答案
阅读快车系列答案【题目】(7分)某地政府急灾民之所需,立即组织12辆汽车,将A、B、C三种救灾物资共92吨一次性运往灾区,甲、乙、丙三种车型的汽车分别运载A、B、C三种物资,每辆车按运载量满装物资。假设装运A、B品种物资的车辆数分别为![]() 、
、![]() ,根据下表提供的信息解答下列问题:
,根据下表提供的信息解答下列问题:
车型 | 甲 | 乙 | 丙 |
汽车运载量(吨/辆) | 5 | 8 | 10 |
(1)装运C品种物资车辆数为 辆(用含![]() 与
与![]() 的代数式表示);
的代数式表示);
(2)试求A、B、C三种物资各几吨。