题目内容
【题目】己知长方形![]() ,
,![]() 为坐标原点,
为坐标原点,![]() 点坐标为
点坐标为![]() ,
,![]() 点在
点在![]() 轴的正半轴上,
轴的正半轴上,![]() 点在
点在![]() 轴的正半轴上,
轴的正半轴上,![]() 是线段
是线段![]() 上的动点,设
上的动点,设![]() ,已知点
,已知点![]() 在第一象限且是直线
在第一象限且是直线![]() 上一点,若
上一点,若![]() 是等腰直角三角形.
是等腰直角三角形.
(![]() )求点
)求点![]() 的坐标并写出解题过程.
的坐标并写出解题过程.
(![]() )直角
)直角![]() 向下平移
向下平移![]() 个单位后,在该直线上是否存在点
个单位后,在该直线上是否存在点![]() ,使
,使![]() 是等腰直角三角形.
是等腰直角三角形.

【答案】(![]() )
)![]() ;(
;(![]() )存在点
)存在点![]() ,使
,使![]() 为等腰直角三角形,
为等腰直角三角形,![]() 坐标为
坐标为![]() ,
,![]() ,
,![]() .
.
【解析】试题分析:
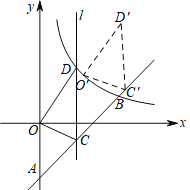
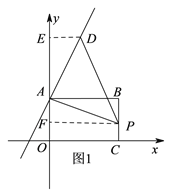
(1)由点D和点A都在直线y=2x+6上可知,若△APD是等腰直角三角形,则只能是点A为直角顶点,如图,过点D作DE⊥y轴于点E,则易证![]() ≌
≌![]() ,由此可得
,由此可得![]() ,
,![]() ,从而可得点D的坐标为(6-m,14),将D的坐标代入y=2x+6中,解得m的值,即可得到点D的坐标;
,从而可得点D的坐标为(6-m,14),将D的坐标代入y=2x+6中,解得m的值,即可得到点D的坐标;
(2)将直线y=2x+6向下平移12个单位所得新直线的解析式为:y=2x-6,由图可知,点A、P在直线y=2x-6两侧,故当△APD为等腰直角三角形时,存在∠ADP=90°,∠APD=90°两种可能情况,其中当∠ADP=90°时,又存在点D在点A的上方和下方两种情况,如图2、图3和图4,然后结合已知条件进行推理计算即可.
试题解析:
(![]() )∵点A、D都在直线y-2x+6上,
)∵点A、D都在直线y-2x+6上,
∴当△APD是等腰直角三角形时,只能是点A为直角顶点,
如图1:过![]() 作
作![]() 轴于
轴于![]() ,
,![]() 轴于
轴于![]() ,
,
∵![]() ,
,
∴![]() ≌
≌![]() ,
,
∴![]() ,
,![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
代入![]() 中得:-2m+6=14,解得:m=2,
中得:-2m+6=14,解得:m=2,
∴![]() ;
;
(![]() )存在点
)存在点![]() ,使
,使![]() 为等腰直角三角形,
为等腰直角三角形,
直线![]() 向下平移
向下平移![]() 个单位后变成
个单位后变成![]() ,
,
当![]() 时,
时,
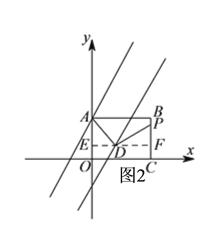
①、如图2所示,过![]() 作
作![]() 交
交![]() 、
、![]() 于
于![]() 、
、![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ≌
≌![]() ,
,
∴![]() ,
,![]() ,
,
设![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,
![]() ,
,
∴![]()
![]() .
.
∴![]() ,
,
代入![]() 中得,
中得,
![]() ,
,
∴![]() .
.
②如图3所示:
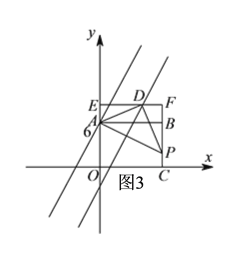
过![]() 作
作![]() 平行线
平行线![]() 交
交![]() 延长线于
延长线于![]() ,
,
∴![]() ≌
≌![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,
代入![]() 中得,
中得,
![]() ,
,
∴![]() .
.
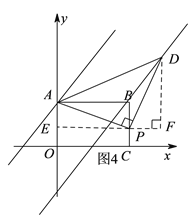
③当![]() 时,如图4,过
时,如图4,过![]() 作
作![]() ,交其垂线
,交其垂线![]() 于
于![]() ,
,
∴![]() ≌
≌![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,
代入![]() 中,
中,
![]() ,
,
∴![]() ,
,
综上所述,点D的坐标为![]() ,
,![]() ,
,![]() .
.

练习册系列答案
相关题目