题目内容
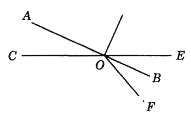
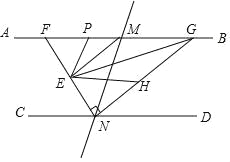
【题目】如图,直线AB∥CD,直线MN与AB,CD分别交于点M,N,ME,NE分别是∠AMN与∠CNM的平分线,NE交AB于点F,过点N作NG⊥EN交AB于点G.
(1)求证:EM∥NG;
(2)连接EG,在GN上取一点H,使∠HEG=∠HGE,作∠FEH的平分线EP交AB于点P,求∠PEG的度数.
【答案】(1)证明见解析;(2)45°.
【解析】
(1)根据平行线的性质以及角平分线得到定义,即可得出∠MEN=90°,再根据NG⊥EN,即可得到∠MEN+∠ENH=180°,进而得到EM∥NG;
(2)先设∠HEG=x,则∠HGE=∠MEG=x,∠NEH=90°-2x,根据EP平分∠FEH,可得∠FEH=2(∠PEG+x),再根据∠FEH+∠HEN=180°,可得方程2(∠PEG+x)+90°-2x=180°,进而解得∠PEG.
解:(1)∵AB∥CD,
∴∠AMN+∠CNM=180°,
∵ME,NE分别是∠AMN与∠CNM的平分线,
∴∠EMN=![]() ∠AMN,∠ENM=
∠AMN,∠ENM=![]() ∠MNC,
∠MNC,
∴∠EMN+∠ENM=90°,即∠MEN=90°,
又∵NG⊥EN,
∴∠MEN+∠ENH=180°,
∴EM∥NG;
(2)设∠HEG=x,则∠HGE=∠MEG=x,∠NEH=90°﹣2x,
∵EP平分∠FEH,
∴∠FEH=2∠PEH=2(∠PEG+x),
又∵∠FEH+∠HEN=180°,
∴2(∠PEG+x)+90°﹣2x=180°,
解得∠PEG=45°.

练习册系列答案
 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案 周周清检测系列答案
周周清检测系列答案
相关题目