题目内容
【题目】(1)问题提出:
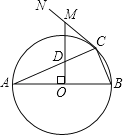
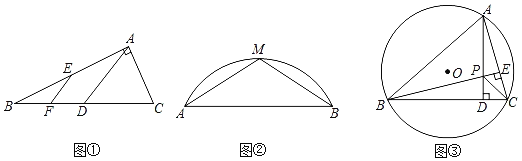
如图①,在Rt△BAC中,∠BAC=90°,点D,E分别是CB,AB的中点,点F是BD的中点,若AB=8,AC=6,则EF= ;
(2)问题探究:
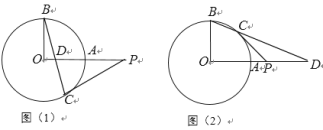
如图②,已知:M是弓形AB上的中点,AB=24,弓形AB的高是8,则对应⊙O的面积为多少?(结果保留根号或π)
(3)问题解决:
如图③,在半径为5的⊙O中,弦BC=8,点A为优弧BC上的动点,过点A作AD⊥BC于点D,过点B作BE⊥AC于点E.AD和BE交于点P,连接PC,试求△PBC面积的最大值.
【答案】(1)![]() ;(2)169π;(3)证明见解析,点P的运动轨迹是弧线,8.
;(2)169π;(3)证明见解析,点P的运动轨迹是弧线,8.
【解析】
(1)如图①中,利用勾股定理求出BC,利用直角三角形斜边中线的性质求出AD,利用三角形的中位线定理即可解决问题.
(2)如图②中,设圆心为O,连接OM,OB,OM交AB于E.设OB=r.利用勾股定理构建方程即可解决问题.
(3)首先证明∠BPC是定值,推出点P的运动轨迹是弧线,如图3-2中,当A,O,D共线时,PD定值最大,此时△PBC的面积最大.
解:(1)如图①中,
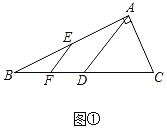
在Rt△ABC中,∵AB=8,AC=6,
∴BC=![]() =10,
=10,
∵BD=CD,
∴AD=![]() BC=5,
BC=5,
∵BE=EA,BF=FD,
∴EF=![]() AD=
AD=![]() ,
,
故答案为![]() .
.
(2)如图②中,设圆心为O,连接OM,OB,OM交AB于E.设OB=r.
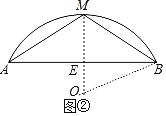
∵![]()
∴OM⊥BA,EM=8,
∴AE=EB=12
在Rt△OEB中,∵OE2+EB2=OB2
∴(r﹣8)2+122=r2,
∴r=13,
∴对应⊙O的面积为169π.
(3)如图3﹣1中,延长CP交AB于F.
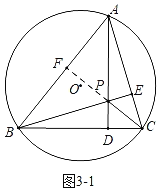
∵在半径为5的⊙O中,弦BC=8,
∴∠BAC是定值,设∠BAC=α,
∵AD,BE是高,
∴CF也是△ABC的高,
∴∠ABE=∠ACF=90°﹣α,
∵∠BPD=∠ABP+∠BAP,∠CPD=∠ACP+∠CAP,
∴∠BPC=∠ABP+∠BAP+∠CAP+∠PCA=90°+90°﹣α=180°﹣α,
∴∠BPC是定值,
∴点P的运动轨迹是弧线,
如图3﹣2中,当A,O,D共线时,PD定值最大,此时△PBC的面积最大.
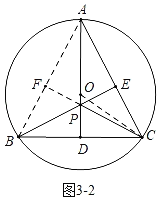
连接OC,在Rt△ODC中,OD=![]() =3,
=3,
∴AD=5+3=8,AC=AB=4![]() ,
,
∵![]() BCAD=
BCAD=![]() ABCF,
ABCF,
∴CF=![]() =
=![]() ,
,
∴AF=![]() =
=![]() ,
,
∵cos∠BAD=![]() =
=![]() ,
,
∴![]() =
=![]() ,
,
∴PA=6,
∴PD=AD﹣PA=2,
∴△PBC的面积的最大值=![]() ×8×2=8.
×8×2=8.

 名校课堂系列答案
名校课堂系列答案【题目】已知二次函数![]() 自变量
自变量![]() 的值和它对应的函数值
的值和它对应的函数值![]() 如下表所示:
如下表所示:
| … | 0 | 1 | 2 | 3 | … |
| … | 3 | 0 |
| 0 | … |
(1)点M是该二次函数图象上一点,若点M纵坐标为8时,求点M的坐标;
(2)设该二次函数图象与![]() 轴的左交点为
轴的左交点为![]() ,它的顶点为
,它的顶点为![]() ,该图象上点
,该图象上点![]() 的横坐标为4,求
的横坐标为4,求![]() 的面积.
的面积.