Question

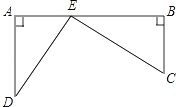
【题目】校车安全是近几年社会关注的热点问题，安全隐患主要是超速和超载．某中学九年级数学活动小组进行了测试汽车速度的实验，如图，先在笔直的公路l旁选取一点A，在公路l上确定点B、C，使得AC⊥l，∠BAC=60°，再在AC上确定点D，使得∠BDC=75°，测得AD=40米，已知本路段对校车限速是50千米/时，若测得某校车从B到C匀速行驶用时10秒，问这辆车在本路段是否超速？请说明理由（参考数据：=1.41，=1.73）

Answer 1

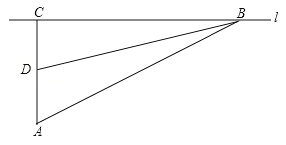
【答案】解：过点D作DE⊥AB于点E，

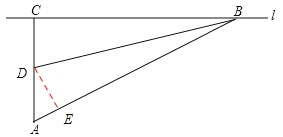
∵∠CDB=75°，∠BAC=60°，∴∠CBD=15°，∠EBD=15°。

在Rt△CBD和Rt△EBD中，

∵∠CBD=∠EBD，∠DCB =∠DEB，BD=BD，

∴△CBD≌△EBD（AAS）。

∴CD=DE。

在Rt△ADE中，∠A=60°，AD=40米，

∴DE=ADsin60°=20米，

∴AC=AD+CD=AD+DE=（40+20）米，

在Rt△ABC中，BC=ACtan∠A=（40+60）米，

∴速度=（米/秒）。

∵12.92米/秒=46.512千米/小时＜50千米/时，∴该车没有超速。

【解析】

试题过点D作DE⊥AB于点E，证明△BCD≌△BED，在Rt△ADE中求出DE，继而得出CD，计算出AC的长度后，在Rt△ABC中求出BC，继而可判断是否超速。