题目内容
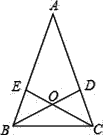
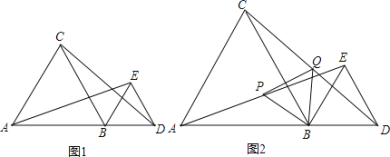
【题目】如图1,点B是线段AD上一点,△ABC和△BDE分别是等边三角形,连接AE和CD.
(1)求证:AE=CD;
(2)如图2,点P、Q分别是AE、CD的中点,试判断△PBQ的形状,并证明.
【答案】(1)见解析(2)见解析
【解析】
(1)根据等边三角形的性质和SAS证明△ABE≌△CBD即可得出结论;
(2)根据△ABE≌△CBD,可得AE=CD,∠EAB=∠DCB,再根据点P、Q分别是AE、CD的中点和SAS即可证明△ABP≌△CBQ,从而得∠PBA=∠QBC,PB=QB,进一步即可推得∠QBP=∠ABC=60°,由此可判断△PBQ的形状.
(1)证明:∵△ABC和△BDE分别是等边三角形,
∴AB=CB,BE=BD,∠ABC=∠DBE=60°,
∴∠ABC+∠CBE=∠DBE+∠CBE,即∠ABE=∠CBD,
在△ABE和△CBD中,
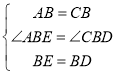 ,
,
∴△ABE≌△CBD(SAS),
∴AE=CD.
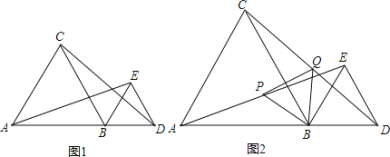
(2)解:△PBQ是等边三角形.
证明如下:由(1)证明可知:△ABE≌△CBD,
∴AE=CD,∠EAB=∠DCB,
∵点P、Q分别是AE、CD的中点,
∴AP=![]() AE,CQ=
AE,CQ=![]() CD,∴AP=CQ,
CD,∴AP=CQ,
在△ABP和△CBQ中,
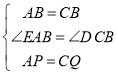 ,
,
∴△ABP≌△CBQ(SAS),
∴∠PBA=∠QBC,PB=QB,
∴∠QBP=∠PBC+∠QBC=∠PBC+∠PBA=∠ABC=60°,
∴△PBQ是等边三角形.

练习册系列答案
相关题目