题目内容
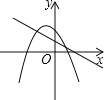
【题目】如图，在平面直角坐标系中，O为原点，一次函数与反比例函数的图象相交于A（2，1）B（－1，－2）两点，与
轴相交于点C．
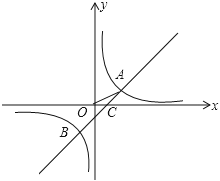
（1）分别求反比例函数和一次函数的解析式（关系式）；
（2）连接OA，求△AOC的面积．
【答案】（1）y=x－1，y=
；（2）
【解析】
（1）利用待定系数法求出反比例函数和一次函数的解析式；（2）求出一次函数求出C的坐标，然后利用三角形的面积公式求面积即可．
解：（1）设一次函数解析式为y1=kx+b（k≠0）；反比例函数解析式为y2=
（a≠0），
∵将A（2，1）、B（﹣1，﹣2）代入y1得：
，
∴
，
∴y1=x﹣1；
∵将A（2，1）代入y2得：a=2，
∴
；
答：反比例函数的解析式是y2=
，一次函数的解析式是y1=x﹣1．
（2）∵一次函数y1=x-1与x轴相交，
∴交点C（1，0），
∴OC=1，
∴S△AOC=
×1×1=．
答：△AOC的面积为．
“点睛”本题主要考查利用待定系数法求函数的解析式，以及三角形面积的求法，综合性比较强．
练习册系列答案
相关题目
【题目】在“新冠病毒”防控期间，某益康医疗器械公司分两次购进酒精消毒液与测温枪两种商品进行销售，两次购进同一商品的进价相同，具体情况如下表所示：
项目 | 购进数量（件） | 购进所需费用（元） | |
酒精消毒液 | 测温枪 | ||
第一次 | 30 | 40 | 8300 |
第二次 | 40 | 30 | 6400 |
（1）求酒精消毒液和测温枪两种商品每件的进价分别是多少元？
（2）公司决定酒精消毒液以每件20元出售，测温枪以每件240元出售．为满足市场需求，需购进这两种商品共1000件，且酒精消毒液的数量不少于测温枪数量的4倍，求该公司销售完上述1000件商品获得的最大利润．
