题目内容
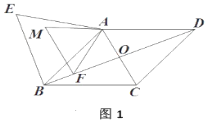
【题目】如图1,在菱形![]() 中,对角线
中,对角线![]() 与
与![]() 相交于点
相交于点![]() ,
,![]() ,
,![]() ,在菱形
,在菱形![]() 的外部以
的外部以![]() 为边作等边三角形
为边作等边三角形![]() .点
.点![]() 是对角线
是对角线![]() 上一动点(点
上一动点(点![]() 不与点
不与点![]() 重合),将线段
重合),将线段![]() 绕点
绕点![]() 顺时针方向旋转
顺时针方向旋转![]() 得到线段
得到线段![]() ,连接
,连接![]() .
.
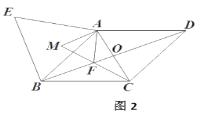
(1)线段![]() 的长为__________;
的长为__________;
(2)如图2,当点![]() 在线段
在线段![]() 上,且点
上,且点![]() ,
,![]() ,
,![]() 三点在同一条直线上时,求证:
三点在同一条直线上时,求证: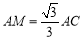 ;
;
(3)连接![]() .若
.若![]() 的周长为
的周长为![]() ,请直接写出
,请直接写出![]() 的面积.
的面积.
【答案】(1)5;(2)证明见解析;(3)25.
【解析】
(1)在RT△OAB中,利用勾股定理求解即可;
(2)由四边形ABCD是菱形,求出△AFM为等边三角形,∠M=∠AFM=60°,再求出∠MAC=90°,在Rt△ACM中利用tan∠M,求出AC;
(3)求出△AEM≌△ABF,利用△AFM的周长求出边长,然后根据勾股定理得出OF,即可得出BF,进而得出△ABF的面积,即可得出![]() 的面积.
的面积.
(1)∵四边形ABCD是菱形,
∴AC⊥BD,OB=OD=![]() BD,
BD,
∵BD=24,
∴OB=12,
在Rt△OAB中,
∵AB=13,
∴OA=![]() ;
;
(2)如图2,
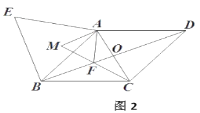
∵四边形ABCD是菱形,
∴BD垂直平分AC,
∴FA=FC,∠FAC=∠FCA,
由已知AF=AM,∠MAF=60°,
∴△AFM为等边三角形,
∴∠M=∠AFM=60°,
∵点M,F,C三点在同一条直线上,
∴∠FAC+∠FCA=∠AFM=60°,
∴∠FAC=∠FCA=30°,
∴∠MAC=∠MAF+∠FAC=60°+30°=90°,
在Rt△ACM中
∵tan∠M=![]() ,
,
∴tan60°=![]() ,
,
∴![]() ;
;
(3)如图,连接EM,
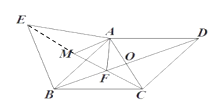
∵△ABE是等边三角形,
∴AE=AB,∠EAB=60°,
由(2)知△AFM为等边三角形,
∴AM=AF,∠MAF=60°,
∴∠EAM=∠BAF,
在△AEM和△ABF中,
 ,
,
∴△AEM≌△ABF(SAS),
∵![]() 的周长为
的周长为![]() ,
,
∴AM=AF=MF=![]() =
=![]()
∴![]()
∴BF=BO-FO=12-2=10
∴![]()
即![]() 的面积为25.
的面积为25.

【题目】下表是二次函数![]() 的
的![]() 的部分对应值:
的部分对应值:
| ··· |
|
|
|
|
|
|
| ··· |
| ··· |
|
|
|
|
|
|
| ··· |
则对于该函数的性质的判断:
①该二次函数有最小值;
②不等式![]() 的解集是
的解集是![]() 或
或![]()
③方程![]() 的实数根分别位于
的实数根分别位于![]() 和
和![]() 之间;
之间;
④当![]() 时,函数值
时,函数值![]() 随
随![]() 的增大而增大;
的增大而增大;
其中正确的是:
A.①②③B.②③C.①②D.①③④
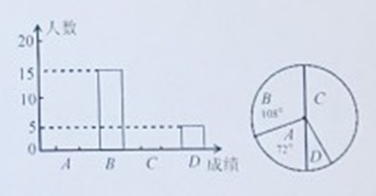
【题目】某校九年级体自模拟测试后,随机抽取了九年级部分学生体有测试成绩进行统计,得到相关的统计图表如下:
成绩/分 |
|
|
|
|
成绩等级 |
|
|
|
|
请根据以上信息解答下列问题:
(1)这次统计共抽取了 名学生的体育测试成绩,补全频数分布直方图
(2)扇形![]() 的圆心角的度数是
的圆心角的度数是
(3)若该校九年级有![]() 名学生,请据此估计该校九年级此次体育测试成绩在
名学生,请据此估计该校九年级此次体育测试成绩在![]() 等级以上(含
等级以上(含![]() 等级)的学生有多少人?
等级)的学生有多少人?
(4)根据测试中存在的问题,通过一段时间的针对性调练,若![]() 等级学生数可提高
等级学生数可提高![]() 等级学生数可提高
等级学生数可提高![]() ,请估计经过训练后九年级体育测试成绩在
,请估计经过训练后九年级体育测试成绩在![]() 等级以上(含
等级以上(含![]() 等级)的学生可达多少人?
等级)的学生可达多少人?
【题目】某公司准备购进一批产品进行销售,该产品的进货单价为6元/个.根据市场调查,该产品的日销售量y(个)与销售单价x(元/个)之间满足一次函数关系.关于日销售量y(个)与销售单价x(元/个)的几组数据如表:
x | 10 | 12 | 14 | 16 |
y | 300 | 240 | 180 | m |
(1)求出y与x之间的函数关系式(不要求写出自变量的取值范围)及m的值.
(2)按照(1)中的销售规律,当销售单价定为17.5元/个时,日销售量为 个,此时,获得日销售利润是 .
(3)为防范风险,该公司将日进货成本控制在900(含900元)以内,按照(1)中的销售规律,要使日销售利润最大,则销售单价应定为多少?并求出此时的最大利润.