题目内容
【题目】如图(13.1),抛物线y=x2+bx+c与x轴交于A,B两点,与y轴交于点C(0,2),连接AC,若tan∠OAC=2.
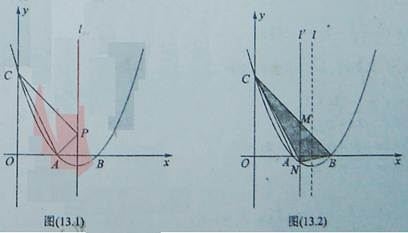
(1)求抛物线对应的二次函数的解析式;
(2)在抛物线的对称轴l上是否存在点P,使∠APC=90°,若存在,求出点P的坐标;若不存在,请说明理由;
(3)如图(13.2)所示,连接BC,M是线段BC上(不与B、C重合)的一个动点,过点M作直线l′∥l,交抛物线于点N,连接CN、BN,设点M的横坐标为t.当t为何值时,△BCN的面积最大?最大面积为多少?
【答案】(1)y=x2-3x+2
(2)点P的坐标为(![]() ,
,![]() )或(
)或(![]() ,
,![]() )
)
(3)1
【解析】
解:(1)∵抛物线y=x2+bx+c过点C(0,2). ∴x=2
又∵tan∠OAC=![]() ="2," ∴OA=1,即A(1,0).
="2," ∴OA=1,即A(1,0).
又∵点A在抛物线y=x2+bx+2上. ∴0=12+b×1+2,b=-3
∴抛物线对应的二次函数的解析式为y=x2-3x+2
(2)存在
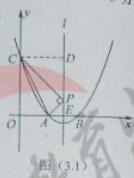
过点C作对称轴l的垂线,垂足为D,如图所示,
∴x=-![]() .∴AE=OE-OA=
.∴AE=OE-OA=![]() -1=
-1=![]() ,∵∠APC=90°,
,∵∠APC=90°,
∴tan∠PAE= tan∠CPD∴![]() ,即
,即![]()
![]() ,解得PE=
,解得PE=![]() 或PE=
或PE=![]() ,
,
∴点P的坐标为(![]() ,
,![]() )或(
)或(![]() ,
,![]() )。(备注:可以用勾股定理或相似解答)
)。(备注:可以用勾股定理或相似解答)
(3)如图,易得直线BC的解析式为:y=-x+2,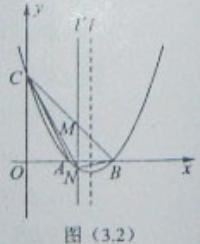
∵点M是直线l′和线段BC的交点,∴M点的坐标为(t,-t+2)(0<t<2)
∴MN=-t+2-(t2-3t+2)="-" t2+2t
∴S△BCM= S△MNC+S△MNB=![]() MNt+
MNt+![]() MN(2-t)
MN(2-t)
=![]() MN(t+2-t)="MN=-" t2+2t(0<t<2),
MN(t+2-t)="MN=-" t2+2t(0<t<2),
∴S△BCN="-" t2+2t=-(t-1)2+1
∴当t=1时,S△BCN的最大值为1。
备注:如果没有考虑的取值范围,可以不扣分)

 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案