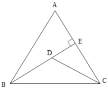
题目内容
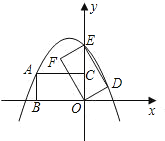
【题目】如图，在
中，
，
于点
，
于点
，
与
交于点
，
于点
，点
是
的中点，连接
并延长交
于点
．
（1）如图①所示，若
，求证：
；
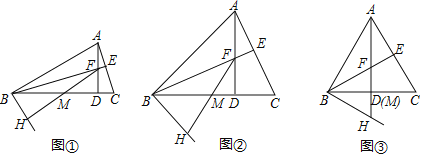
（2）如图②所示，若
，如图③所示，若
（点与点重合），猜想线段
、与
之间又有怎样的数量关系？请直接写出你的猜想，不需证明．
【答案】（1）见解析（2）
【解析】
（1）连接CF，由垂心的性质得出CF⊥AB，证出CF∥BH，由平行线的性质得出∠CBH=∠BCF，证明△BMH≌△CMF得出BH=CF，由线段垂直平分线的性质得出AF=CF，得出BH=AF，AD=DF+AF=DF+BH，由直角三角形的性质得出AD=
BD，即可得出结论；
（2）同（1）可证：AD=DF+AF=DF+BH，再由等腰直角三角形的性质和含30°角的直角三角形的性质即可得出结论．
（1）证明：连接
，如图①所示：
， 
，
，
，
，
，
点
是
的中点，
，
在
和
中，
，
，
，
，，
垂直平分
，
，
，
，
在
中，
，
，
；
（2）解：图②猜想结论：；理由如下：
同（1）可证： 
，
在中，
，
，
；
图③猜想结论：
；理由如下：
同（1）可证：，
在中，
，
，
．
练习册系列答案
相关题目
