题目内容
【题目】如图，已知AB是⊙O的弦，OB = 2，∠B = 30°，C是弦AB上任意一点（不与点A、B重合），连接CO并延长CO交⊙O于点D，连接AD．
（1）弦长AB = ____________（结果保留根号）；
（2）当∠D = 20°时，求∠BOD的度数；
（3）当AC的长度为多少时，以点A、C、D为顶点的三角形与以B、C、O为顶点的三角形相似？请写出解答过程．
【答案】（1）2
（2）100°（3）AC=．
【解析】试题分析：（1）过点O作OE⊥AB于E，则AE=BE=
AB，在Rt△BOE中，利用∠B的余弦可求出BE的长，然后可得出AB的长；（2）连接OA，根据OA=OD=OB,可得∠D =∠DAO =" 20°," ∠B=∠BAO = 30°,然后可求出∠DAB = 50°,再利用圆周角定理可得∠BOD=2∠DAB = 100°；（3）利用三角形的外角的性质可得∠BCO=
∠A+∠D，然后分析可得出只能是△DAC∽△BOC，此时∠DCA=∠BCO=90°，∠DAC=60°，在Rt△BOE中，利用∠DAC的三角函数值可求出AC的长．
试题解析：解：（1）过点O作OE⊥AB于E，
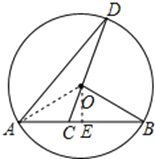
则AE=BE=AB，∠OEB=90°，
∵OB=2，∠B=30°，∴BE=OBcos∠B=2×
=
，
∴AB=2；故答案为：2；
（2）连接OA，
∵OA=OB，OA=OD，∴∠BAO=∠B，∠DAO=∠D，
∴∠DAB=∠BAO+∠DAO=∠B+∠D，
又∵∠B=30°，∠D=20°，
∴∠DAB=50°，
∴∠BOD=2∠DAB=100°；
（3）∵∠BCO=∠A+∠D，
∴∠BCO＞∠A，∠BCO＞∠D，
∴要使△DAC与△BOC相似，只能∠DCA=∠BCO=90°，
此时∠BOC=60°，∠BOD=120°，∴∠DAC=60°，∴△DAC∽△BOC，
∵∠BCO=90°，即OC⊥AB，∴AC=
AB=．
∴当AC的长度为时，以A、C、D为顶点的三角形与以B、C、0为顶点的三角形相似．
