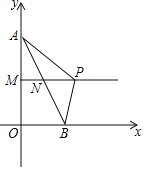题目内容
【题目】如图,四边形ABCD是长方形,∠A=∠ABC=∠BCD=∠CDA=90°,AB∥CD,AD∥BC,E是边AD上一动点.
(1)若∠ECD=2∠ECB,求∠AEC的度数.
(2)若∠ABD=70°,△DEF是等腰三角形,求∠ECB的度数.
(3)若△EFD的面积为4,若△DCF的面积为6,则四边形ABFE的面积为_______.

【答案】(1)∠AEC=150°;(2)20°或80°;(3)11.
【解析】
(1)由∠ECD=2∠ECB和∠BCD=90°可得:∠ECD=60o,∠BCE=30o,再由平行线的性质可得到∠AEC=150°;
(2)由∠ABD=70o得到∠ADB=20o,当EF=DF时,∠DEF=20o;当DE=DF时,∠DEF=80o,再由平行线的性质得到∠ECB=∠DEF;
(3) 由在矩形ABCD中,△EFD的面积为4,△FCD的面积为6,根据等高三角形的面积比等于对应底的比,即可求得EF:FEC,易得△DEF∽△BEC,然后由相似三角形面积比等于相似比的平方,即可求得△BFC的面积,继而求得答案.
(1)∵∠ECD=2∠ECB和∠BCD=90°,
∴∠ECD=60o,∠BCE=30o,
又∵AD//BC,
∴∠AEC+∠BCE=180o,
∴∠AEC=150°;
(2)∵∠ABD=70o,∠A=90o,
∴∠ADB=20o,
又∵△DEF是等腰三角形,
∴DE=DF或EF=DF,
当EF=DF时,∠FED=∠EDF=20o,
当DE=DF时,∠DEF=80o,
又∵AD//BC,
∴∠EBC=∠DEF,
∴∠EBC=20o或80o;
(3) ∵△EFD的面积为4,△FECD的面积为6,
∴EF:FC=4:6=2:3,
∵四边形ABCD是矩形,
∴AD∥BC,
∴△DEF∽△BFC,
∴S△DEF:S△BFC=(![]() )2=4:9,
)2=4:9,
∴S△BFC=9,
∴S△ABD=S△BCD=S△BFC+S△CDE=15,
∴S阴影=S△ABD-S△DEF=15-4=11.

【题目】某超市销售每台进价分别为200元、150元的甲、乙两种型号的电器,下表是近两周的销售情况:
销售时段 | 销售数量 | 销售收入 | |
甲种型号 | 乙种型号 | ||
第一周 | 3台 | 5台 | 1900元 |
第二周 | 4台 | 10台 | 3200元 |
(进价、售价均保持不变,利润=销售收入-进货成本)
⑴求A、B两种型号的电风扇的销售单价;
⑵若超市准备用不多于5000元的金额再采购这两种型号的电风扇共30台,且按(1)中的销售单价全部售完利润不少于1850元,则有几种购货方案?
⑶在⑵的条件下,超市销售完这30台电风扇哪种方案利润最大?最大利润是多少?请说明理由.