题目内容
【题目】如果方程x2+px+q=0有两个实数根x1, x2,那么x1+x2=﹣p,x1x2=q,请根据以上结论,解决下列问题:
(1)已知a、b是方程x2+15x+5=0的二根,则![]() =?
=?
(2)已知a、b、c满足a+b+c=0,abc=16,求正数c的最小值.
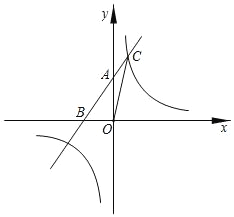
(3)结合二元一次方程组的相关知识,解决问题:已知![]() 和
和![]() 是关于x,y的方程组
是关于x,y的方程组![]() 的两个不相等的实数解.问:是否存在实数k,使得y1y2﹣
的两个不相等的实数解.问:是否存在实数k,使得y1y2﹣![]() =2?若存在,求出的k值,若不存在,请说明理由.
=2?若存在,求出的k值,若不存在,请说明理由.
【答案】(1)43(2)4(3)存在,当k=﹣2时,![]()
【解析】
(1)根据a,b是x2+15x+5=0的解,求出a+b和ab的值,即可求出![]() 的值.
的值.
(2)根据a+b+c=0,abc=16,得出a+b=-c,ab=![]() ,a、b是方程x2+cx+
,a、b是方程x2+cx+![]() =0的解,再根据c2-4
=0的解,再根据c2-4![]() ≥0,即可求出c的最小值.
≥0,即可求出c的最小值.
(3)运用根与系数的关系求出x1+x2=1,x1x2=k+1,再解y1y2-![]() =2,即可求出k的值.
=2,即可求出k的值.
(1)∵a、b是方程x2+15x+5=0的二根,
∴a+b=﹣15,ab=5,
∴![]() =
=![]() =
=![]() =43,
=43,
故答案是:43;
(2)∵a+b+c=0,abc=16,
∴a+b=﹣c,ab=![]() ,
,
∴a、b是方程x2+cx+![]() =0的解,
=0的解,
∴c2﹣4![]() ≥0,c2﹣
≥0,c2﹣![]() ≥0,
≥0,
∵c是正数,
∴c3﹣43≥0,c3≥43 , c≥4,
∴正数c的最小值是4.
(3)存在,当k=﹣2时,![]() .
.
由x2﹣y+k=0变形得:y=x2+k,
由x﹣y=1变形得:y=x﹣1,把y=x﹣1代入y=x2+k,并整理得:x2﹣x+k+1=0,
由题意思可知,x1 , x2是方程x2﹣x+k+1=0的两个不相等的实数根,故有:
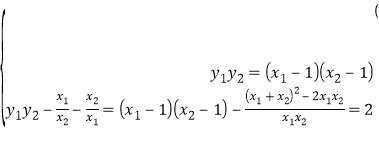
即: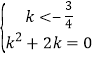
解得:k=﹣2.

练习册系列答案
相关题目