题目内容
【题目】如图,矩形ABCD中,AB=12cm,BC=24cm,如果将该矩形沿对角线BD折叠,那么图中阴影部分的面积( )cm2 . 
A.72
B.90
C.108
D.144
【答案】B
【解析】解:由折叠得到△BCD≌△BC′D,由矩形ABCD得到△ABD≌△CDB,∴△ABD≌△C′DB,
∴∠C′BD=∠ADB,
∴EB=DE,
在△ABE和△C′DE中,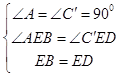 ,
,
∴△ABE≌△C′DE(AAS),
∴AE=C′E,
设AE=C′E=xcm,则有ED=AD﹣AE=(24﹣x)cm,
在Rt△ABE中,根据勾股定理得:AB2+AE2=BE2 , 即122+x2=(24﹣x)2 ,
解得:x=9,
∴AE=9cm,ED=15cm,
则S△BED= ![]() EDAB=
EDAB= ![]() ×15×12=90(cm2).
×15×12=90(cm2).
故选B
【考点精析】解答此题的关键在于理解翻折变换(折叠问题)的相关知识,掌握折叠是一种对称变换,它属于轴对称,对称轴是对应点的连线的垂直平分线,折叠前后图形的形状和大小不变,位置变化,对应边和角相等.

练习册系列答案
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案
相关题目