题目内容
【题目】如图,已知,EG∥AF,请你从下面三个条件中,再选出两个作为已知条件,另一个作为结论,推出一个正确的命题.并证明这个命题(只写出一种情况)①AB=AC ②DE=DF ③BE=CF
已知:EG∥AF, , .
求证: .
证明:
【答案】AB=AC;DE=DF;BE=CF;作EG∥AF交BC于G,
∴∠EGB=∠ACB,∠GED=∠CFD,
∵AB=AC,
∴∠B=∠ACB,
∴∠B=∠EGB,
∴EB=EG,
在△EGD和△FCD中,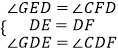 ,
,
∴EG=CF,
∴BE=CF
【解析】已知:EG∥AF,AB=AC,DE=DF.求证:BE=CF.
证明:作EG∥AF交BC于G,
∴∠EGB=∠ACB,∠GED=∠CFD,
∵AB=AC,
∴∠B=∠ACB,
∴∠B=∠EGB,
∴EB=EG,
在△EGD和△FCD中,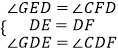 ,
,
∴△EGD≌△FCD,
∴EG=CF,
∴BE=CF.
故答案为:AB=AC;DE=DF;BE=CF;作EG∥AF交BC于G,
∴∠EGB=∠ACB,∠GED=∠CFD,
∵AB=AC,
∴∠B=∠ACB,
∴∠B=∠EGB,
∴EB=EG,
在△EGD和△FCD中,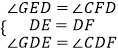 ,
,
∴EG=CF,
∴BE=CF
作EG∥AF交BC于G,根据平行线的性质得到∠EGB=∠ACB,∠GED=∠CFD,证明△EGD≌△FCD,根据全等三角形的性质解答即可.

练习册系列答案
 步步高达标卷系列答案
步步高达标卷系列答案
相关题目

