题目内容
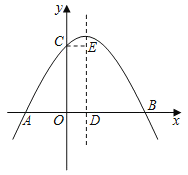
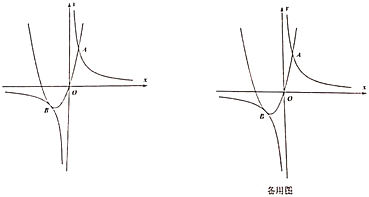
【题目】如图,抛物线![]() (
(![]() )与双曲线
)与双曲线![]() 相交于点
相交于点![]() 、
、![]() ,已知点
,已知点![]() 坐标
坐标![]() ,点
,点![]() 在第三象限内,且
在第三象限内,且![]() 的面积为3(
的面积为3(![]() 为坐标原点).
为坐标原点).
(1)求实数![]() 、
、![]() 、
、![]() 的值;
的值;
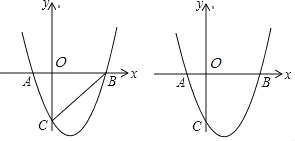
(2)在该抛物线的对称轴上是否存在点![]() 使得
使得![]() 为等腰三角形?若存在请求出所有的
为等腰三角形?若存在请求出所有的![]() 点的坐标,若不存在请说明理由.
点的坐标,若不存在请说明理由.
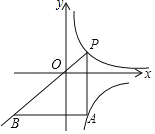
(3)在坐标系内有一个点![]() ,恰使得
,恰使得![]() ,现要求在
,现要求在![]() 轴上找出点
轴上找出点![]() 使得
使得![]() 的周长最小,请求出
的周长最小,请求出![]() 的坐标和
的坐标和![]() 周长的最小值.
周长的最小值.
【答案】(1)![]() ,
,![]() ;(2)存在,
;(2)存在,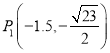 ,
,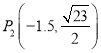 ,
,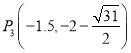 ,
,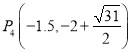 ,
,![]() ;(3)
;(3)![]()
【解析】
(1)由点A在双曲线上,可得k的值,进而得出双曲线的解析式.设![]() (
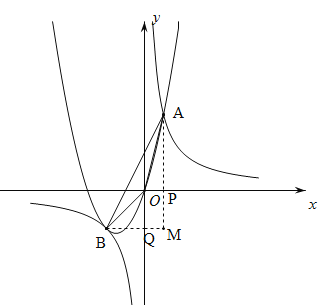
(![]() ),过A作AP⊥x轴于P,BQ⊥y轴于Q,直线BQ和直线AP相交于点M.根据
),过A作AP⊥x轴于P,BQ⊥y轴于Q,直线BQ和直线AP相交于点M.根据![]() =3解方程即可得出k的值,从而得出点B的坐标,把A、B的坐标代入抛物线的解析式即可得到结论;
=3解方程即可得出k的值,从而得出点B的坐标,把A、B的坐标代入抛物线的解析式即可得到结论;
(2)抛物线对称轴为![]() ,设
,设![]() ,则可得出
,则可得出![]() ;
;![]() ;
;![]() .然后分三种情况讨论即可;
.然后分三种情况讨论即可;
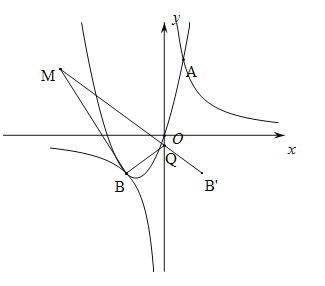
(3)设M(x,y).由MO=MA=MB,可求出M的坐标.作B关于y轴的对称点B'.连接B'M交y轴于Q.此时△BQM的周长最小.用两点间的距离公式计算即可.
(1)由![]() 知:k=xy=1×4=4,
知:k=xy=1×4=4,
∴![]() .
.
设![]() (
(![]() ).
).
过A作AP⊥x轴于P,BQ⊥y轴于Q,直线BQ和直线AP相交于点M,则S△AOP=S△BOQ=2.
![]()
![]()
![]()
![]()
令:![]() ,
,
整理得:![]() ,
,
解得:![]() ,
,![]() .
.
∵m<0,
∴m=-2,
故![]() .
.
把A、B带入![]()
![]()
解出:![]() ,
,
∴![]() .
.
(2)![]()
∴抛物线![]() 的对称轴为
的对称轴为![]() .
.
设![]() ,则
,则![]() ,
,![]() ,
,![]() .
.
∵△POB为等腰三角形,
∴分三种情况讨论:
①![]() ,即
,即![]() ,解得:
,解得:![]() ,
,
∴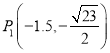 ,
,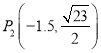 ;
;
②![]() ,即
,即![]() ,解得:
,解得:![]() ,
,
∴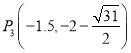 ,
,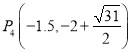 ;
;
③![]() ,即
,即![]() ,解得:
,解得:![]()
∴![]() ;
;
(3)设![]() .
.
∵![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,![]() .
.
∵![]() ,
,
∴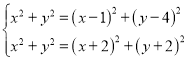
解得: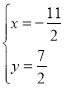 ,
,
∴![]() .
.
作B关于y轴的对称点B'坐标为:(2,-2).
连接B'M交y轴于Q.此时△BQM的周长最小.
![]()
![]() =MB'+MB
=MB'+MB
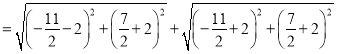
![]() .
.

练习册系列答案
相关题目