题目内容
如图1,点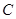 将线段
将线段 分成两部分,如果
分成两部分,如果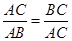 ,那么称点
,那么称点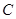 为线段
为线段 的黄金分割点.
的黄金分割点.
某研究小组在进行课题学习时,由黄金分割点联想到“黄金分割线”,类似地给出“黄金分割线”的定义:直线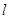 将一个面积为
将一个面积为 的图形分成两部分,这两部分的面积分别为
的图形分成两部分,这两部分的面积分别为 ,
,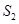 ,如果
,如果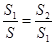 ,那么称直线
,那么称直线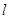 为该图形的黄金分割线.
为该图形的黄金分割线.

(1)研究小组猜想:在 中,若点
中,若点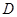 为
为 边上的黄金分割点(如图2),则直线
边上的黄金分割点(如图2),则直线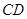 是
是 的黄金分割线.你认为对吗?为什么?
的黄金分割线.你认为对吗?为什么?
(2)请你说明:三角形的中线是否也是该三角形的黄金分割线?
(3)研究小组在进一步探究中发现:过点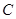 任作一条直线交
任作一条直线交 于点
于点 ,再过点
,再过点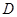 作直线
作直线 ,交
,交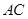 于点
于点 ,连接
,连接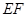 (如图3),则直线
(如图3),则直线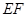 也是
也是 的黄金分割线.
的黄金分割线.
请你说明理由.
(4)如图4,点 是
是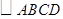 的边
的边 的黄金分割点,过点
的黄金分割点,过点 作
作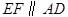 ,交
,交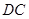 于点
于点 ,显然直线
,显然直线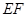 是
是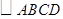 的黄金分割线.请你画一条
的黄金分割线.请你画一条 的黄金分割线,使它不经过
的黄金分割线,使它不经过 各边黄金分割点.
各边黄金分割点.
(1)对,理由见解析(2)不可能(3)理由见解析(4)见解析
【解析】(1)直线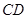 是
是 的黄金分割线.理由如下:
的黄金分割线.理由如下:
设 的边
的边 上的高为
上的高为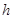 .
.
 ,
, ,
,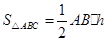 ,
,
所以, ,
, .··············· 2分
.··············· 2分
又因为点 为边
为边 的黄金分割点,所以有
的黄金分割点,所以有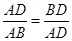 .因此
.因此 .
.
所以,直线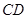 是
是 的黄金分割线.·············· 4分
的黄金分割线.·············· 4分
(2)因为三角形的中线将三角形分成面积相等的两部分,此时 ,即
,即
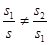 ,所以三角形的中线不可能是该三角形的黄金分割线.········ 6分
,所以三角形的中线不可能是该三角形的黄金分割线.········ 6分
(3)因为 ,所以
,所以 和
和 的公共边
的公共边 上的高也相等,
上的高也相等,
所以有 .························· 7分
.························· 7分
设直线 与
与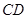 交于点
交于点 .所以
.所以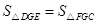 .
.
所以
 ,
,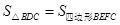 .
.
又因为 ,所以
,所以 .··········· 9分
.··········· 9分
因此,直线 也是
也是 的黄金分割线.··············· 10分
的黄金分割线.··············· 10分
(4)画法不惟一,现提供两种画法;·················· 12分

画法一:如答图1,取 的中点
的中点 ,再过点
,再过点 作一条直线分别交
作一条直线分别交 ,
, 于
于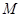 ,
,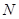 点,则直线
点,则直线 就是
就是 的黄金分割线.
的黄金分割线.
画法二:如答图2,在 上取一点
上取一点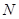 ,连接
,连接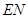 ,再过点
,再过点 作
作 交
交 于点
于点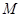 ,连接
,连接 ,则直线
,则直线 就是
就是 的黄金分割线.
的黄金分割线.
(1)由于 是同高,而点
是同高,而点 为边
为边 的黄金分割点,则
的黄金分割点,则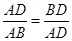 ,所以
,所以 ,故直线
,故直线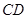 是
是 的黄金分割线
的黄金分割线
(2)只需判断它们面积比是否相等,若相等则中线是三角形的黄金分割线,否则不是
(3)根据平行线间的距离相等,则 ,通过图形面积的转化,直线
,通过图形面积的转化,直线 分三角形的图形面积有
分三角形的图形面积有 ,故直线
,故直线 也是
也是 的黄金分割线
的黄金分割线
(4)画法不惟一,只需分成图形面积比相等即可

 如图,C、D两点将线段AB分成2:3:4三部分,E为线段AB的中点,AD=6cm.
如图,C、D两点将线段AB分成2:3:4三部分,E为线段AB的中点,AD=6cm. 如图,长度为24cm的线段AB的中点为C,D点将线段BC分成两部分,且CD:DB=1:2,则线段AD的长为( )
如图,长度为24cm的线段AB的中点为C,D点将线段BC分成两部分,且CD:DB=1:2,则线段AD的长为( ) 将线段
将线段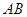 分成两部分,如果
分成两部分,如果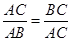 ,那么称点
,那么称点 将一个面积为
将一个面积为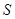 的图形分成两部分,这两部分的面积分别为
的图形分成两部分,这两部分的面积分别为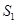 ,
,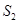 ,如果
,如果 ,那么称直线
,那么称直线
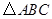 中,若点
中,若点 为
为 是
是 ,再过点
,再过点 ,交
,交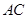 于点
于点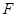 ,连接
,连接 (如图3),则直线
(如图3),则直线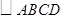 的边
的边 ,交
,交 于点
于点