题目内容
 如图,长度为24cm的线段AB的中点为C,D点将线段BC分成两部分,且CD:DB=1:2,则线段AD的长为( )
如图,长度为24cm的线段AB的中点为C,D点将线段BC分成两部分,且CD:DB=1:2,则线段AD的长为( )分析:先根据线段中点定义得到AC=BC=
AB=12cm,再利用CD:DB=1:2可计算出CD=
BC=4cm,然后利用AD=AC+CD进行计算即可.
| 1 |
| 2 |
| 1 |
| 3 |
解答:解:∵线段AB的中点为C,
∴AC=BC=
AB=
×24=12(cm),
∵CD:DB=1:2,
∴CD=
BC=
×12=4(cm),
∴AD=AC+CD=12cm+4cm=16cm.
故选D.
∴AC=BC=
| 1 |
| 2 |
| 1 |
| 2 |
∵CD:DB=1:2,
∴CD=
| 1 |
| 3 |
| 1 |
| 3 |
∴AD=AC+CD=12cm+4cm=16cm.
故选D.
点评:本题考查了两点间的距离:连接两点间的线段的长度叫两点间的距离.

练习册系列答案
 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案
相关题目
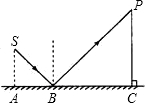 如图,有点光源S在平面镜上方,若在P点看到点光源的反射光线,并测得AB=10cm,BC=20cm,PC⊥AC,且PC=24cm,点光源S到平面镜的距离即SA的长度为( )
如图,有点光源S在平面镜上方,若在P点看到点光源的反射光线,并测得AB=10cm,BC=20cm,PC⊥AC,且PC=24cm,点光源S到平面镜的距离即SA的长度为( )| A、11cm | B、12cm | C、13cm | D、14cm |
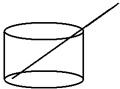 将一根24cm的筷子,置于底面直径为15cm,高8cm的圆柱形水杯中,如图所示,设筷子露在杯子外面的长度hcm,则h的取值范围是( )
将一根24cm的筷子,置于底面直径为15cm,高8cm的圆柱形水杯中,如图所示,设筷子露在杯子外面的长度hcm,则h的取值范围是( )| A、h≤17cm | B、h≥8cm | C、15cm≤h≤16cm | D、7cm≤h≤16cm |
 如图所示,有点光源S在平面镜上面,若在P点看到点光源的反射光线,并测得AB=10cm,BC=20cm,PC⊥AC,且PC=24cm,则点光源S到平面镜的距离即SA的长度为
如图所示,有点光源S在平面镜上面,若在P点看到点光源的反射光线,并测得AB=10cm,BC=20cm,PC⊥AC,且PC=24cm,则点光源S到平面镜的距离即SA的长度为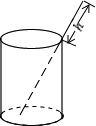 将一根24cm的筷子,置于底面直径为15cm,高8cm的圆柱形水杯中,如图所示,设筷子露在杯子外面的长度为hcm,则h的取值范围是
将一根24cm的筷子,置于底面直径为15cm,高8cm的圆柱形水杯中,如图所示,设筷子露在杯子外面的长度为hcm,则h的取值范围是