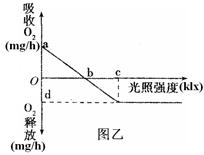
题目内容
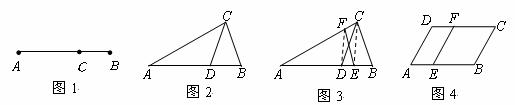
 如图,C、D两点将线段AB分成2:3:4三部分,E为线段AB的中点,AD=6cm.
如图,C、D两点将线段AB分成2:3:4三部分,E为线段AB的中点,AD=6cm.求:(1)线段AB的长:(2)线段DE的长.
分析:(1)根据比值可设AC=2x,CD=3x,BD=4x.根据AD=6,列方程求解;
(2)根据E为线段AB的中点,求得AE的长,则DE=AD-AE.
(2)根据E为线段AB的中点,求得AE的长,则DE=AD-AE.
解答:解:(1)设AC=2x,CD=3x,BD=4x.
则有2x+3x=6,x=1.2.
则AB=2x+3x+4x=9x=10.8(cm).
(2)∵E为线段AB的中点,
∴AE=
AB=5.4.
∴DE=AD-AE=6-5.4=0.6(cm).
则有2x+3x=6,x=1.2.
则AB=2x+3x+4x=9x=10.8(cm).
(2)∵E为线段AB的中点,
∴AE=
| 1 |
| 2 |
∴DE=AD-AE=6-5.4=0.6(cm).
点评:此题能够用一个未知数表示出图中的三条线段,利用方程求解,理解线段的中点的概念.

练习册系列答案
 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案
相关题目
 将线段
将线段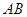 分成两部分,如果
分成两部分,如果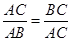 ,那么称点
,那么称点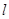 将一个面积为
将一个面积为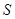 的图形分成两部分,这两部分的面积分别为
的图形分成两部分,这两部分的面积分别为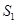 ,
,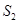 ,如果
,如果 ,那么称直线
,那么称直线
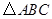 中,若点
中,若点 为
为 是
是 ,再过点
,再过点 ,交
,交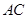 于点
于点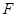 ,连接
,连接 (如图3),则直线
(如图3),则直线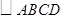 的边
的边 ,交
,交 于点
于点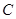 将线段
将线段 分成两部分,如果
分成两部分,如果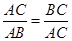 ,那么称点
,那么称点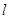 将一个面积为
将一个面积为 的图形分成两部分,这两部分的面积分别为
的图形分成两部分,这两部分的面积分别为 ,
,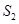 ,如果
,如果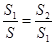 ,那么称直线
,那么称直线
 中,若点
中,若点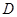 为
为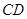 是
是 ,再过点
,再过点 ,交
,交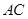 于点
于点 ,连接
,连接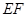 (如图3),则直线
(如图3),则直线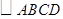 的边
的边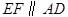 ,交
,交 于点
于点