题目内容
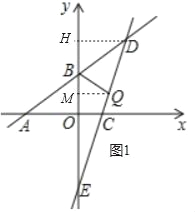
【题目】已知:如图,一次函数![]() 的图象分别与x轴、y轴相交于点A、B,且与经过点C(2,0)的一次函数y=kx+b的图象相交于点D,点D的横坐标为4,直线CD与y轴相交于点E.
的图象分别与x轴、y轴相交于点A、B,且与经过点C(2,0)的一次函数y=kx+b的图象相交于点D,点D的横坐标为4,直线CD与y轴相交于点E.
(1)直线CD的函数表达式为 ;(直接写出结果)
(2)点Q为线段DE上的一个动点,连接BQ.
①若直线BQ将△BDE的面积分为1:2两部分,试求点Q的坐标;
②将△BQD沿着直线BQ翻折,使得点D恰好落在直线AB下方的坐标轴上,请直接写出点Q的坐标: .

【答案】(1)y=3x﹣6;(2)①(![]() ,﹣2)或(
,﹣2)或(![]() ,2);②存在,点Q的坐标为(3,3)或(
,2);②存在,点Q的坐标为(3,3)或(![]() ,
,![]() ).
).
【解析】
(1)求出C、D两点坐标即可解决问题;
(2)①分两种情形S△BEQ=![]() S△BDE或S△BEQ=
S△BDE或S△BEQ=![]() S△BDE分别构建方程即可;
S△BDE分别构建方程即可;
②分两种情形:当点D落在x正半轴上(记为点D1)时,如图2中;当点D落在y负半轴上(记为点D2)时,如图3中;分别求解即可.
解:(1)由题意:D(4,6),C(2,0),
设直线CD的解析式为y=kx+b,
则有![]() ,
,
解得![]() ,
,
∴直线CD的解析式为y=3x﹣6,
故答案为:y=3x﹣6;
(2)①∵直线BQ将△BDE的面积分为1:2两部分,
∴S△BEQ=![]() S△BDE或S△BEQ=
S△BDE或S△BEQ=![]() S△BDE,
S△BDE,
在y=![]() x+3中,当x=0时,y=3;当x=4时,y=6,
x+3中,当x=0时,y=3;当x=4时,y=6,
∴B(0,3),D(4,6).
在y=3x﹣6中,当x=0时,y=﹣6,
∴E(0,﹣6),
∴BE=9,
如图1中,过点D作DH⊥y轴于点H,则DH=4,
∴S△BDE=![]() BEDH=
BEDH=![]() ×9×4=18,
×9×4=18,
∴S△BEQ=![]() ×18=6或S△BEQ=
×18=6或S△BEQ=![]() ×18=12,
×18=12,
设Q(t,3t﹣6),由题意知t>0,
过点Q作QM⊥y轴于点M,则QM=t,
∴![]() ×9×t=6或
×9×t=6或![]() ×9×t=12,
×9×t=12,
解得t=![]() 或
或![]() ,
,
当t=![]() 时,3t﹣6=﹣2,
时,3t﹣6=﹣2,
当t=![]() 时3t﹣6=2,
时3t﹣6=2,
∴Q的坐标为(![]() ,﹣2)或(
,﹣2)或(![]() ,2);
,2);
②当点D落在x正半轴上(记为点D1)时,如图2中,
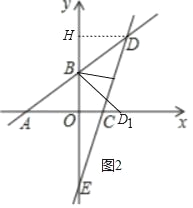
由(2)知B(0,3),D(4,6),
∴BH=BO=3,
由翻折得BD=BD1,
在△Rt△DHB和Rt△D1OB中,
![]() ,
,
∴Rt△DHB≌Rt△D1OB(HL),
∴∠DBH=∠D1BO,
由翻折得∠DBQ=∠D1BQ,
∴∠HBQ=∠OBQ=90°,
∴BQ∥x轴,
∴点Q的纵坐标为3,
在y=3x﹣6中,当y=3时,x=3,
∴Q(3,3);
当点D落在y负半轴上(记为点D2)时,如图3中,
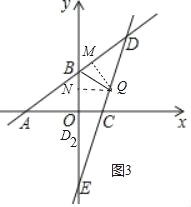
过点Q作QM⊥BD,QN⊥OB,垂足分别为点M、N,
由翻折得∠DBQ=∠D2BQ,
∴QM=QN,
由(2)知S△BDE=18,即S△BQD+S△BQE=18,
∴![]() BDQM+
BDQM+![]() BEQN=18,
BEQN=18,
由两点之间的距离公式,得BD=![]() =5,
=5,
∴![]() ×5QN+
×5QN+![]() ×9QN=18,
×9QN=18,
解得QN=![]() ,
,
∴点Q的横坐标为![]() ,
,
在y=3x﹣6中,当x=时,y=
![]() ,
,
∴Q(![]() ,
,![]() ).
).
综合知,点Q的坐标为(3,3)或(![]() ,
,![]() ).
).