题目内容
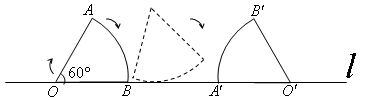
如图,P是的⊙O半径OA上的一点,D在⊙O上,且PD=PO.过点D作⊙O的切线交OA的延长线于点C,延长DP交⊙O于K,连接KO、OD.
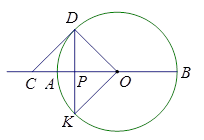
(1)证明:PC=PD;
(2)若该圆半径为5,CD//KO,请求出OC的长.

(1)证明:PC=PD;
(2)若该圆半径为5,CD//KO,请求出OC的长.
(1)先根据等边对等角得到∠1=∠2,再根据切线的性质得到CD⊥OD,即可得到∠3+∠1=90°,再根据∠CDP+∠2=90°可得∠3=∠CDP,从而可以证得结论;(2)

试题分析:(1)先根据等边对等角得到∠1=∠2,再根据切线的性质得到CD⊥OD,即可得到∠3+∠1=90°,再根据∠CDP+∠2=90°可得∠3=∠CDP,从而可以证得结论;
(2)先根据“ASA”判定△CPD≌△OPK,从而得到CD=OK,再根据勾股定理即可求得OC的值.
(1)如图

∵PD=PO
∴∠1=∠2
∵CD是⊙O的切线
∴CD⊥OD
∴∠3+∠1=90°
又∵∠CDP+∠2=90°
∴∠3=∠CDP
∴PC=PD;
(2)∵CD∥KO,有∠3=∠POK,
由(1)得,CP=PD=PO,又∠CPD=∠KPO
∴△CPD≌△OPK
∴CD=OK=5
在Rt△COD中,
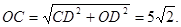
点评:本题知识点较多,综合性强,是中考常见题,难度不大,学生需熟练掌握圆的基本性质.

练习册系列答案
相关题目
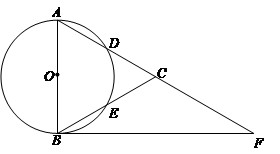
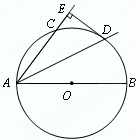
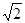 ㎝,AC=
㎝,AC= ㎝,则∠BAC的度数为 .
㎝,则∠BAC的度数为 .
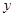 轴右侧⊙A优弧上一点,则
轴右侧⊙A优弧上一点,则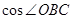 的值是________________.
的值是________________.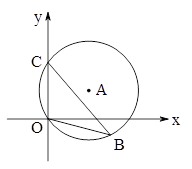
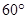 的扇形纸片
的扇形纸片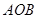 ,在直线
,在直线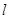 上向右作无滑动的滚动至扇形
上向右作无滑动的滚动至扇形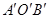 处,则顶点
处,则顶点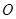 经过的路线总长为 。
经过的路线总长为 。