题目内容
如图，PA，PB是⊙O是切线，A，B为切点， AC是⊙O的直径，若∠BAC=25°，则∠P= _度.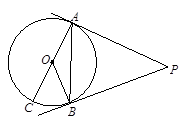
50
试题分析：先根据圆的基本性质求∠BOA的度数，再根据切线的性质和四边形的内角和定理求解即可.
∵OA=OB，∠BAC=25°
∴∠BOA=130°
∵PA，PB是⊙O是切线
∴∠PAO=∠PBO=90°
∠P=360°-∠BOA-∠PAO-∠PBO=50°.
点评：解题的关键是熟练掌握切线垂直于经过切点的半径；四边形的内角和等于360°.
练习册系列答案
相关题目
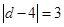，且两圆的半径是方程
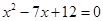的两个根，试判断这两圆的位置关系.
