题目内容
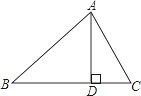
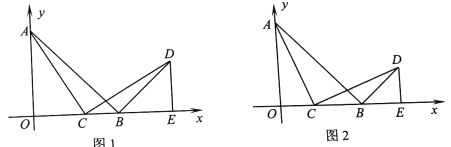
【题目】如图1，在平面直角坐标系中，OA＝OB，点B的坐标为(1，0)，AB＝
，线段OB上的动点(点C不与O、B重合)，连接AC,作AC⊥CD,作DE⊥x轴，垂足为点E.
(1)求证:△ACO≌△CDE;
(2)猜想△BDE的形状，并证明结论:
(3)如图2,当△BCD为等腰三角形时，求点D的坐标.
【答案】（1）见详解；（2）等腰直角三角形；（3）（
，-1）
【解析】
（1）根据垂直的定义得到∠ACD=90°，根据余角的性质得到∠ACO=∠CDE，根据全等三角形的判定定理即可得到结论；
（2）根据全等三角形的性质得到AO=CE，CO=DE，求得OB=CE，得到OC+CB=BE+CB，由等腰直角三角形的判定定理即可得到结论；
（3）设D点的纵坐标为m，当△BCD为等腰三角形时，①BC=BD，②CD=BD=m，③当CD=BC＞CE根据题意列方程即可得到结论．
解：（1）∵AC⊥CD，
∴∠ACD=90°，
∴∠ACO+∠DCE=90°，
∵作DE⊥x轴，AO⊥OB，
∴∠DEC=∠COA=90°，
∴∠CDE+∠DCE=90°，
∴∠ACO=∠CDE，
在△ACO与△CDE中
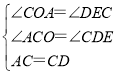
∴△ACO≌△CDE（AAS）；
（2）△BDE为等腰直角三角形，
理由：∵△ACO≌△CDE，
∴AO=CE，CO=DE，
∵OA=CE，CO=DE，
∵OA=OB，
∴OB=CE，
∴OC+CB=BE+CB，
即OC=BE=DE，
∵∠DEB=90°，
∴△BDE是等腰直角三角形；
（3）解：设D点的纵坐标为m，
当△BCD为等腰三角形时，
①BC=BD，∵△BDE是等腰直角三角形，
∴DE=BE=m，
∴BD=BC=m，
∵CE=AO=1，
∴m+m=1，
∴m=-1，
∴D（，-1）；
②CD=BD=m，
∵OC=DE=m，
∴AC=CD=
m，
解得：m=±1（舍去），
③当CD=BC＞CE（这种情况不存在0，
综上所述，当△BCD为等腰三角形时，点D的坐标（，-1）．
