题目内容
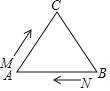
【题目】如图，
中，
，现有两点M、N分别从点A、点B同时出发，沿三角形的边运动，已知点M的速度为
，点N的速度为
当点N第一次到达B点时，M、N同时停止运动．
点M，N运动几秒后，M、N两点重合？
点M、N运动几秒后，可得到等边三角形
？
当点M、N在BC边上运动时，能否得到以MN为底边的等腰三角形AMN？如存在，请求出此时M、N运动的时间．
【答案】
点M，N运动24秒后，M、N两点重合；
点M、N运动4秒后，可得到等边
；
当M、N运动16秒后，得到以MN为底边的等腰三角形AMN．
【解析】
由点N运动路程
点M运动路程
间的路程，列出方程，可求t的值；
由等边三角形的性质可得
，可列方程，即可求x的值；
由全等三角形的性质可得
，可列方程，可求y的值．
设运动t秒，M、N两点重合，
根据题意得：
答：点M，N运动24秒后，M、N两点重合
设点M、N运动x秒后，可得到等边
是等边三角形
，
解得：
点M、N运动4秒后，可得到等边三角形．
设M、N运动y秒后，得到以MN为底边的等腰三角形AMN．
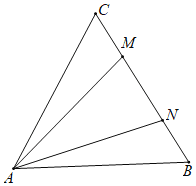
是等边三角形
，
是等腰三角形
，且
，
，
≌
答：当M、N运动16秒后，得到以MN为底边的等腰三角形AMN．
练习册系列答案
相关题目
