题目内容
【题目】如图1,在正方形ABCD中,点E,F分别是边AB,BC上的点,且BE=CF.连结CE,DF.将线段FD绕点F逆时针旋转90°,得到线段FG.
(1)依题意将图1补全;
(2)连结EG,请判断:EG与CF的数量关系是 ,位置关系是 ;并证明你的结论;
(3)当FG经过BE中点时,写出求∠CDF度数的思路.

【答案】(1)见解析(2)EG与CF的数量关系是:EG=CF,位置关系是:EG∥CF;(3)当FG经过BE中点P时
【解析】分析:(1)根据要求画出图形即可;
(2)只要证明四边形EGFC是平行四边形即可;
(3)首先证明![]() ,求出
,求出![]() 即可解决问题.
即可解决问题.
详解:(1)如图所示:
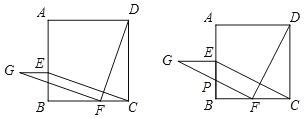 ;
;
(2)EG与CF的数量关系是:EG=CF,位置关系是:EG∥CF;
证明:∵正方形ABCD,
∴BC=CD,![]()
∵BE=CF,
∴△BCE≌△CDF
∴DF=CE,∠BEC=∠CFD.
∵![]()
∴![]()
即CE⊥DF,
∵线段FD绕点F逆时针旋转![]() ,得到线段FG,
,得到线段FG,
∴CE∥FG,DF=FG.
∴CE=FG.
∴四边形GFCE是平行四边形。
∴EG=CF,EG∥CF;
故答案为EG=CF,EG∥CF.
(3)当FG经过BE中点P时,
由△BCE≌△CDF,可得∠CDF=∠BCE.
由![]() ,可得∠BCE=∠G.
,可得∠BCE=∠G.
即∠CDF═∠G,
由BE=CF=GE,可得![]()
利用锐角三角函数,可求∠G的度数,从而可求∠CDF的度数.

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案
相关题目