题目内容
【题目】如图,已知点A(﹣2,0),点B(6,0),点C在第一象限内,且△OBC为等边三角形,直线BC交y轴于点D,过点A作直线AE⊥BD于点E,交OC于点E
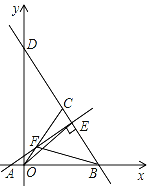
(1)求直线BD的解析式;(2)求线段OF的长;(3)求证:BF=OE.
【答案】(1)![]() ;(2)OF= 2;(3)见解析.
;(2)OF= 2;(3)见解析.
【解析】
(1)在Rt△ABD中,通过解直角三角形可求出OD的长,进而可得出点D的坐标,再根据点B,D的坐标,利用待定系数法可求出直线BD的解析式;
(2)由等边三角形的性质结合三角形内角和定理,可得出∠BAE=∠CFE=30°,进而可得出∠OAF=∠OFA=30°,再利用等角对等边可得出线段OF的长;
(3)通过解含30度角的直角三角形可求出BE的长,结合BC的长可得出CE=OF=2,由OB=CO,∠BOF=∠OCE及OF=CE可证出△OBF≌△COE(SAS),再利用全等三角形的性质可得出BF=OE.
(1)∵△OBC为等边三角形,
∴∠ABC=60°.
在Rt△ABD中,tan∠ABD=![]() ,即
,即![]() ,
,
∴AD=![]() ,
,
∴点D的坐标是(0,![]() ).
).
设BD的解析式是y=kx+b(k≠0),
将B(6,0),D(0,![]() )代入y=kx+b,得:
)代入y=kx+b,得: ,
,
解得: ,
,
∴直线BD的解析式为![]() .
.
(2)解:∵AE⊥BC,△OBC是正三角形,
∴∠BAE=∠CFE=30°,
∴∠OAF=∠OFA=30°,
∴OF=OA=2,即OF的长为2.
(3)证明:∵AB=8,∠OBC=60°,AE⊥BC,
∴BE=![]() AB=4,
AB=4,
∴CE=BC-BE=6-4=2,
∴OF=CE.
在△OBF和△COE中, ,
,
∴△OBF≌△COE(SAS),
∴BF=OE.

练习册系列答案
 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案
相关题目