题目内容
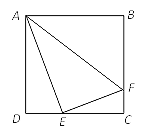
【题目】如图,已知正方形ABCD的边长为8,点E是DC上的一动点,过点作EF⊥AE,交BC于点F,连结AF.
(1)证明:△ADE∽△ECF;
(2)若△ADE的周长与△ECF的周长之比为4:3,求BF的长.
【答案】(1)详见解析;(2)6.5.
【解析】
(1)根据正方形的性质证明∠FEC =∠DAE,即可求解;
(2)根据周长比得到相似比,故![]() ,求出FC,即可求解.
,求出FC,即可求解.
解: (1)∵四边形ABCD是正方形
∴∠C =∠D=90°, AD=DC=8,
∵EF⊥AC,
∴∠AEF=90°,
∴∠AED +∠FED =90°
在Rt△ADE中,∠DAE+∠AED =90°
∴∠FEC =∠DAE
∴ △DAE∽△FEC
(2) ∵△DAE∽△FEC
∴![]()
∵△ADE的周长与△ECF的周长之比为4:3
∴△ADE的边长与△ECF的边长之比为4:3
即![]()
∵AD =8, ∴EC=6
∴DE=8-6=2
∴![]()
∴FC =1.5
∴DF =8-1.5=6.5

【题目】某大型水果超市销售无锡水蜜桃,根据前段时间的销售经验,每天的售价x(元/箱)与销售量y(箱)有如表关系:
每箱售价x(元) | 68 | 67 | 66 | 65 | … | 40 |
每天销量y(箱) | 40 | 45 | 50 | 55 | … | 180 |
已知y与x之间的函数关系是一次函数.
(1)求y与x的函数解析式;
(2)水蜜桃的进价是40元/箱,若该超市每天销售水蜜桃盈利1600元,要使顾客获得实惠,每箱售价是多少元?
(3)七月份连续阴雨,销售量减少,超市决定采取降价销售,所以从7月17号开始水蜜桃销售价格在(2)的条件下,下降了m%,同时水蜜桃的进货成本下降了10%,销售量也因此比原来每天获得1600元盈利时上涨了2m%(m<100),7月份(按31天计算)降价销售后的水蜜桃销售总盈利比7月份降价销售前的销售总盈利少7120元,求m的值.