题目内容
13、观察下列各式并找规律,再猜想填空:(a+b)(a2-ab+b2)=a3+b3,(x+2y)(x2-2xy+4y2)=x3+8y3
则(2a+3b)(4a2-6ab+9b2)=
则(2a+3b)(4a2-6ab+9b2)=
8a3+27b3
.分析:左边为一个二项式与一个三项式相乘,左边二项式中间加减号与三项式中间第二项加减号正好相反,二项式两项为三项式第一第三项的一次项.
解答:解:(2a+3b)(4a2-6ab+9b2),
=(2a)3+(3b)3,
=8a3+27b3.
故答案为:8a3+27b3.
=(2a)3+(3b)3,
=8a3+27b3.
故答案为:8a3+27b3.
点评:本题考查了完全平方式,是信息题,两数的和乘以这两个数的平方和减去它们的差,等于这两个数的立方和(或两数的差乘以这两个数的平方和加上它们的和,等于这两个数的立方差),读懂题目信息是求解的关键.

练习册系列答案
相关题目
 ,
,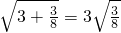 ,
, ,
,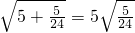 ,…
,…