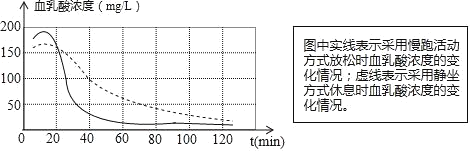
��Ŀ����
����Ŀ��ij��Ʒ�Ľ���Ϊÿ��40Ԫ���ۼ�ÿ��������60Ԫ��ÿ��������80Ԫ.���ۼ�Ϊÿ��60Ԫ�ǣ�ÿ���¿�����100�������ÿ����Ʒ���ۼ�ÿ����1Ԫ����ÿ��������2��.��ÿ����Ʒ���ۼ�Ϊ![]() Ԫ��
Ԫ��![]() Ϊ����������ÿ���µ���������Ϊ
Ϊ����������ÿ���µ���������Ϊ![]() Ԫ.
Ԫ.
��1����![]() ��
��![]() �ĺ�����ϵʽ��ֱ��д���Ա���
�ĺ�����ϵʽ��ֱ��д���Ա���![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
��2��ÿ����Ʒ���ۼ۶�Ϊ����Ԫʱ��ÿ���¿ɻ��������������������Ƕ���Ԫ��
��3����ÿ����Ʒ����Ϊ����Ԫʹ��ÿ���µ�����ǡΪ2250Ԫ��
���𰸡���1��![]()
![]() ����
����![]() ��
��![]() Ϊ����������2��ÿ����Ʒ���ۼ۶�Ϊ75Ԫʱ��ÿ���¿ɻ���������������������2450Ԫ����3��ÿ����Ʒ���ۼ�Ϊ65Ԫʱ��ÿ���µ�����ǡΪ2250Ԫ.
Ϊ����������2��ÿ����Ʒ���ۼ۶�Ϊ75Ԫʱ��ÿ���¿ɻ���������������������2450Ԫ����3��ÿ����Ʒ���ۼ�Ϊ65Ԫʱ��ÿ���µ�����ǡΪ2250Ԫ.
��������
��1�������ۼ�Ϊ60ʱ��ÿ������100�����ۼ�����Ӱ����������˸���60��x��80��ʽ��⣻
��2���ɣ�1������õĺ�������ʽ�������Ա���x�ķ�Χ����������ֵ��
��3����60��x��80����y=2250����ö���x��ֵ��
��1��![]()
![]() ����
����![]() ��
��![]() ������
������
��2��![]()
![]() ��
��
��![]() ���൱
���൱![]() ʱ��
ʱ��![]() �����ֵ2450.
�����ֵ2450.
��ÿ����Ʒ���ۼ۶�Ϊ75Ԫʱ��ÿ���¿ɻ���������������������2450Ԫ.
��3����![]() Ԫʱ��
Ԫʱ��![]() ��
��
��ã�![]() ��
��![]() ������
�����У�![]() ���������⣬��ȥ.
���������⣬��ȥ.
��˵�ÿ����Ʒ���ۼ�Ϊ65Ԫʱ��ÿ���µ�����ǡΪ2250Ԫ.

����Ŀ��1��̽������Ӻ���5m����������1m/min���ٶ�����.���ͬʱ��2��̽������Ӻ���15m����������0.5m/min���ٶ�����.������������������50min.����������ʱ��Ϊx(x��0).
(��)�������⣬��д�±�
����ʱ��/min | 10 | 30 | �� | x |
1��̽����������λ�õĺ���/m | 15 | �� | ||
2��̽����������λ�õĺ���/m | 30 | �� |
(��)��ijʱ�����������ܷ�λ��ͬһ�߶ȣ�����ܣ���ʱ���������˶ʱ�䣿λ��ʲô�߶ȣ�������ܣ���˵������.
(��)��0��x��50ʱ��������������λ�õĺ�������������ף�