题目内容
【题目】已知,点O到△ABC的两边AB、AC所在直线的距离相等,且OB=OC.
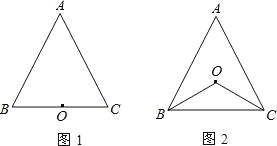
(1)如图1,若点O在BC上,求证:△ABC是等腰三角形.
(2)如图2,若点O在△ABC内部,求证:AB=AC.
(3)若点O点在△ABC的外部,△ABC是等腰三角形还成立吗?请画图表示.
【答案】(1)证明见解析;(2)证明见解析;(3)若O点在△ABC的外部,AB=AC不一定成立;图形见解析.
【解析】
(1)首先过点O作OD⊥AB于D,作OE⊥AC于E,易证得Rt△BOD≌Rt△COE,即可得∠B=∠C,根据等角对等边的性质,即可得证;
(2)首先过点O作OD⊥AB于D,作OE⊥AC于E,易证得Rt△BOD≌Rt△COE,然后又由OB=OC,根据等边对等角的性质,易证得∠ABC=∠ACB,根据等角对等边的性质,AB=AC;
(3)首先过点O作OD⊥AB于D,作OE⊥AC的延长线于点E,易证得Rt△BOD≌Rt△COE,然后又由OB=OC,根据等边对等角的性质,易证得∠ABC=∠ACB,根据等角对等边的性质,AB=AC.
(1)证明:如图1,
过O作OE⊥AB于E,OF⊥AC于F,
则∠OEB=∠OFC=90°,
∵点O到△ABC的两边AB、AC所在直线的距离相等,
∴OE=OF,
在Rt△OEB和Rt△OFC中,
![]() ,
,
∴Rt△OEB≌Rt△OFC(HL),
∴∠ABC=∠ACB,
∴AB=AC;
(2)证明:如图2,过O作OE⊥AB于E,OF⊥AC于F,
则∠OEB=∠OFC=90°,
∵点O到△ABC的两边AB、AC所在直线的距离相等,
∴OE=OF,
在Rt△OEB和Rt△OFC中,
![]() ,
,
∴Rt△OEB≌Rt△OFC(HL),
∴∠ABO=∠ACO,
∵∠OBC=∠OCB,
∴∠ABC=∠ACB,
∴AB=AC;
(3)解:若O点在△ABC的外部,AB=AC不一定成立,
理由是:①当∠A的平分线和BC的垂直平分线重合时,如图3,
过O作OE⊥AB交AB的延长线于E,OF⊥AC交AC的延长线于F,
则∠OEB=∠OFC=90°,
∵点O到△ABC的两边AB、AC所在直线的距离相等,
∴OE=OF,
在Rt△OEB和Rt△OFC中
![]()
∴Rt△OEB≌Rt△OFC(HL),
∴∠EBO=∠FCO,
∵OB=OC,
∴∠OBC=∠OCB,
∵∠ABC=180°﹣(∠OBC+∠EBO),∠ACB=180°﹣(∠OCB+∠FCO),
∴∠ABC=∠ACB,
∴AB=AC;
②当∠A的平分线和BC的垂直平分线不重合时,如图④,
此时∠ABC和∠ACB不相等,
∴AB≠AC,
∴△ABC是等腰三角形不一定成立.