Question

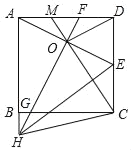
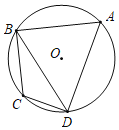
【题目】已知如图，⊙O的半径为4，四边形ABCD为⊙O的内接四边形，且∠C＝2∠A．

（1）求∠A的度数．

（2）求BD的长．

Answer 1

【答案】（1）60°；（2）．

【解析】

（1）根据圆内接四边形的性质即可得到结论；

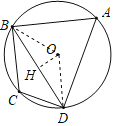
（2）连接OB，OD，作OH⊥BD于H根据已知条件得到∠BOD＝120°；求得∠OBD＝∠ODB＝30°，解直角三角形即可得到结论．

（1）∵四边形ABCD为⊙O的内接四边形，

∴∠C+∠A＝180°，

∵∠C＝2∠A，

∴∠A＝60°；

（2）连接OB，OD，作OH⊥BD于H

∵∠A＝60°，∠BOD＝2∠A，

∴∠BOD＝120°；

又∵OB＝OD，

∴∠OBD＝∠ODB＝30°，

∵OH⊥BD于H，

在Rt△DOH中，，即，

∴，

∵OH⊥BD于H，

∴.