Question

【题目】函数的图象的对称轴为直线.

（1）求的值；

（2）将函数的图象向右平移2个单位，得到新的函数图象．

①直接写出函数图象的表达式；

②设直线与轴交于点A，与y轴交于点B,当线段AB与图象只有一个公共点时，直接写出的取值范围.

Answer 1

【答案】（1）m=3；（2）①；②.

【解析】

（1）根据二次函数的对称轴公式可得关于m的方程，解方程即可求出结果；

（2）①根据抛物线的平移规律解答即可；

②根据二次函数的性质以及一次函数的性质，结合图象只要满足直线与y轴的交点的纵坐标大于抛物线与y轴交点的纵坐标解答即可.

解：（1）∵的对称轴为直线，∴，解得：m=3；

（2）①∵函数的表达式为y=x2－2x+1，即为，

∴图象向右平移2个单位得到的新的函数图象的表达式为；

②∵直线y＝﹣2x+2t（t＞m）与x轴交于点A，与y轴交于点B，

∴A（t，0），B（0，2t），

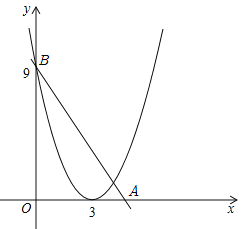
∵新的函数图象G的顶点为（3，0），与y的交点为（0，9），

∴当线段AB与图象G只有一个公共点时，如图，2t＞9，解得t＞，

故t的取值范围是t＞．