Question

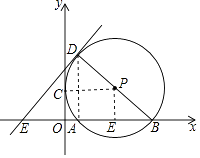
【题目】如图，已知⊙P与x轴交于A和B（9，0）两点，与y轴的正半轴相切与点C（0，3），作⊙P的直径BD，过点D作直线DE⊥BD，交x轴于E点，若点P在双曲线y= 上，则直线DE的解析式为 ．

Answer 1

【答案】y= x+
【解析】解：连接PC．AD，过P作PE⊥AB于E， ∵C（0，3），B（9，0），
∴OB=9，OC=3，
∵⊙P与y轴的正半轴相切与点C，
∴PC⊥y轴，
∴四边形OEPC是矩形，
∴PE=OC=3，
把y=3代入y= 得，x=5，
∴P（5，3），
∴PC=5，BD=10，
∵BD是⊙P的直径，
∴AD⊥x轴，
∴PE∥AD，
∵P是BD的中点，
∴AD=6，
∴AB=8，
∴OA=1，
∴D（1，6），
∵DE⊥BD，
∴∠EDA+∠BDA=∠AED+∠EDA=90°，
∴∠AED=∠ADB，
∴△ADE∽△ABD，
∴ ，
∴AE= ，
∴E（﹣ ，0），
设直线DE的解析式为y=kx+b，
∴ ，
∴ ，
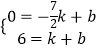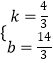∴直线DE的解析式为y= x+ ．
所以答案是：y= x+ ．

【考点精析】通过灵活运用切线的性质定理，掌握切线的性质：1、经过切点垂直于这条半径的直线是圆的切线2、经过切点垂直于切线的直线必经过圆心3、圆的切线垂直于经过切点的半径即可以解答此题．