Question

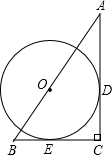如图，Rt△ABC中，∠ACB=90°，AC=4，BC=2，以AB上的一点O为圆心分别与均AC，BC相切于点D、E．
①求⊙O的半径；
②求sin∠BOC的值．

Answer 1

分析：（1）连接OD，OE，根据S_△AOC+S_△BOC=S_△ABC，即

1

2

AC•OD+

1

2

BC•OE=

1

2

AC•BC即可求解；
（2）过点C作CF⊥AB，垂足为F，在Rt△ABC与Rt△OEC中，根据勾股定理求出AB，OC，根据三角形ABC的面积等于

1

2

AC•BC=

1

2

AB•CF，就可以求出CF的值，就可以求出sin∠BOC的值．

解答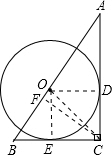：解：（1）连接OD，OE，设OD=r
∵AC，BC切⊙O于D，E
∴∠ODC=∠OEC=90°，OD=OE
∵S_△AOC+S_△BOC=S_△ABC
∴

1

2

AC•OD+

1

2

BC•OE=

1

2

AC•BC
即

1

2

×4r+

1

2

×2r=

1

2

×4×2，
∴r=

4

3

．
（2）过点C作CF⊥AB，垂足为F，连接OC，
在Rt△ABC与Rt△OEC中
AB=

42+22

=2

5

，OC=

( 4 3 )2+( 4 3 )2

=

4

3

2

∵

1

2

AC•BC=

1

2

AB•CF
∴CF=

AC•BC

AB

=

4 5

5

∴sin∠BOC=

CF

OC

=

4 5

5

×

3

4 2

=

3 10

10

即sin∠BOC=

3 10

10

．

点评：本题考查的是切线性质的实际应用，运用切线的性质可证明四边形ODCE正方形．根据三角形的面积的公式就可以求解．