Ő‚ńŅńŕ»›
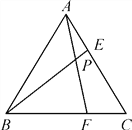
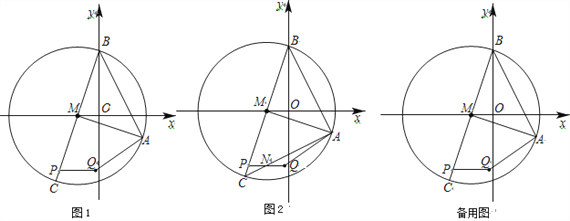
°ĺŐ‚ńŅ°Ņ“—÷™£ļ»ÁÕľ1£¨‘ŕ∆Ĺ√ś÷ĪĹ«◊ÝĪÍŌĶ÷–£¨A£®2£¨£≠1£©£¨“‘M£®£≠1£¨0£©ő™‘≤–ń£¨“‘AMő™įŽĺ∂Ķń‘≤ĹĽy÷Š”ŕĶ„B£¨Ń¨ĹŠBM≤Ę—”≥§ĹĽ°—M”ŕĶ„C£¨∂ĮĶ„P‘ŕŌŖ∂őBC…Ō‘ň∂Į£¨≥§ő™![]() ĶńŌŖ∂őPQ°őx÷Š£®Ķ„Q‘ŕĶ„P”“≤ŗ£©£¨Ń¨ĹŠAQ£ģ
ĶńŌŖ∂őPQ°őx÷Š£®Ķ„Q‘ŕĶ„P”“≤ŗ£©£¨Ń¨ĹŠAQ£ģ
£®1£©«ů°—MĶńįŽĺ∂≥§ļÕĶ„BĶń◊ÝĪÍ£Ľ
£®2£©»ÁÕľ2£¨Ń¨ĹŠAC£¨ĹĽŌŖ∂őPQ”ŕĶ„N£¨
ĘŔ«ůACňý‘ŕ÷ĪŌŖĶńĹ‚őŲ Ĺ£Ľ
ĘŕĶĪPN=QN Ī£¨«ůĶ„QĶń◊ÝĪÍ£Ľ
£®3£©Ķ„P‘ŕŌŖ∂őBC…Ō‘ň∂ĮĶńĻż≥Ő÷–£¨«Ž÷ĪĹ”–ī≥ŲAQĶń◊Ó–°÷ĶļÕ◊Óīů÷Ķ£ģ
°ĺīūįł°Ņ£®1£©įŽĺ∂ő™![]() £¨Ķ„B£®0£¨3£©£Ľ
£¨Ķ„B£®0£¨3£©£Ľ
£®2£©ĘŔyAC£Ĺ![]() x£≠2£¨ĘŕĶ„Q◊ÝĪÍő™£®£≠
x£≠2£¨ĘŕĶ„Q◊ÝĪÍő™£®£≠![]() £¨£≠
£¨£≠ ![]() £©
£©
£®3£©AQ◊Ó–°÷Ķő™![]() £¨AQ◊Óīů÷Ķő™
£¨AQ◊Óīů÷Ķő™![]()
°ĺĹ‚őŲ°Ņ ‘Ő‚∑÷őŲ£ļ(1)°ĘĻżĶ„A◊ųAE°Õx÷Š£¨‘ÚAE£Ĺ1£¨ME£Ĺ3£¨ī”∂ÝĶ√≥Ų‘≤ĶńįŽĺ∂£¨»Ľļůłýĺ›Rt°ųMOBĶńĻīĻ…∂®ņŪĶ√≥ŲOBĶń≥§∂»£¨Ķ√≥ŲĶ„BĶń◊ÝĪÍ£Ľ(2)°Ę ◊Ō»…Ť÷ĪŌŖACĶńĹ‚őŲ Ĺő™£ļy=kx+b£¨łýĺ›÷––ń∂‘≥∆Ķń–‘÷ Ķ√≥ŲĶ„CĶń◊ÝĪÍ£¨ņŻ”√īż∂®ŌĶ ż∑®«ů≥ŲļĮ żĹ‚őŲ Ĺ£Ľłýĺ›Ő‚“‚Ķ√≥Ų÷ĪŌŖBCĶńĹ‚őŲ Ĺő™y=3x+3£¨…ŤĶ„PĶń◊ÝĪÍő™(x£¨3x+3)£¨ī”∂ÝĶ√≥ŲĶ„NĶń◊ÝĪÍ£¨»Ľļůłýĺ›Ķ„N‘ŕ÷ĪŌŖAC…Ō«ů≥ŲxĶń÷Ķ£¨ī”∂ÝĶ√≥ŲĶ„QĶń◊ÝĪÍ£Ľ(3)°Ęłýĺ›◊Ó–°÷ĶļÕ◊Óīů÷ĶĶńľ∆ň„∑®‘Ú“‘ľįĻīĻ…∂®ņŪĶ√≥Ų◊Ó÷Ķ.
‘Ő‚Ĺ‚őŲ£ļ£®1£©ĻżĶ„A◊ųAE°Õx÷Š£¨‘ÚAE£Ĺ1£¨ME£Ĺ3£¨°ŗAM£Ĺ![]() £¨ľīįŽĺ∂ő™
£¨ľīįŽĺ∂ő™![]()
ňý“‘BM£Ĺ![]() £¨°ŖOM£Ĺ1£¨°ŗOB£Ĺ3£¨ľīĶ„B£®0£¨3£©
£¨°ŖOM£Ĺ1£¨°ŗOB£Ĺ3£¨ľīĶ„B£®0£¨3£©
£®2£©ĘŔ…ŤĹ‚őŲ Ĺő™…ŤyAC£Ĺkx£ęb ”…Ő‚“‚Ķ√Ķ„C”ŽĶ„BĻō”ŕĶ„M≥…÷––ń∂‘≥∆£¨
°ŗĶ„C£®£≠2£¨£≠3£© ”÷Ķ„A£®2£¨£≠1£©
ľīĶĪx£Ĺ2 Ī£¨y£Ĺ£≠1£ĽĶĪx£Ĺ£≠2 Ī£¨y£Ĺ£≠3 Ĺ‚Ķ√k£Ĺ![]() £¨b£Ĺ£≠2 °ŗyAC£Ĺ
£¨b£Ĺ£≠2 °ŗyAC£Ĺ![]() x£≠2
x£≠2
ĘŕŅ…«ůyBC£Ĺ3x£ę3£¨…ŤĶ„P£®x£¨3x£ę3£© ”…Ő‚“‚Ķ√Ķ„Nő™(x£ę![]() £¨3x£ę3)
£¨3x£ę3)
°ŖĶ„N¬š‘ŕAC…Ō£¨ňý“‘3x£ę3£Ĺ![]() ( x£ę
( x£ę![]() )£≠2 Ĺ‚Ķ√x£Ĺ£≠
)£≠2 Ĺ‚Ķ√x£Ĺ£≠![]()
ňý“‘Ķ„Q◊ÝĪÍő™£®£≠![]() £¨£≠
£¨£≠![]() £©
£©
£®3£©AQ◊Ó–°÷Ķő™![]() £¨ AQ◊Óīů÷Ķő™
£¨ AQ◊Óīů÷Ķő™![]()

 Ķŕ1ĺŪĶ•‘™‘¬Ņľ∆ŕ÷–∆ŕń©ŌĶŃ–īūįł
Ķŕ1ĺŪĶ•‘™‘¬Ņľ∆ŕ÷–∆ŕń©ŌĶŃ–īūįł