题目内容
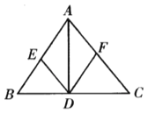
【题目】如图,已知:AD是△ABC的角平分线,DE//AC交AB于E,DF//AB交AC于F,
(1)求证:四边形AEDF是菱形;
(2)当△ABC满足什么条件时,四边形AEDF是正方形?请说明理由.
【答案】(1)见详解;(2)见详解.
【解析】
(1)根据DE∥AC交AB于点E,DF∥AB交AC于点F,可以判断四边形AEDF是平行四边形,再根据角平分线的性质和平行线的性质即可证明结论成立;
(2)根据有一个角是直角的菱形是正方形可以解答本题.
(1)证明:∵DE∥AC交AB于点E,DF∥AB交AC于点F,
∴四边形AEDF是平行四边形,∠EAD=∠ADF,
∵AD是△ABC的角平分线,
∴∠EAD=∠FAD,
∴∠ADF=∠FAD,
∴FA=FD,
∴四边形AEDF是菱形(有一组邻边相等的平行四边形是菱形);
(2)解:当△ABC是直角三角形,∠BAC=90°,时,四边形AEDF是正方形,
理由:∵△ABC是直角三角形,∠BAC=90°,
由(1)知四边形AEDF是菱形,
∴四边形AEDF是正方形(有一个角是直角的菱形是正方形).

练习册系列答案
相关题目