题目内容
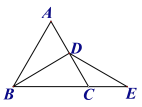
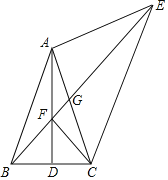
【题目】在△ABC中,AB=AC,D是BC的中点,以AC为腰向外作等腰直角△ACE,∠EAC=90°,连接BE,交AD于点F,交AC于点G.
(1)若∠BAC=50°,求∠AEB的度数;
(2)求证:∠AEB=∠ACF;
(3)试判断线段EF、BF与AC三者之间的等量关系,并证明你的结论.
【答案】(1)20°;(2)证明见解析;(3)EF2+BF2=2AC2.理由见解析.
【解析】
(1)根据等腰直角三角形的旋转得出∠ABE=∠AEB,求出∠BAE,根据三角形内角和定理求出即可;
(2)根据等腰三角形的性质得出∠BAF=∠CAF,根据SAS推出△BAF≌△CAF,根据全等得出∠ABF=∠ACF,即可得出答案;
(3)根据全等得出BF=CF,求出∠CFG=∠EAG=90°,根据勾股定理求出EF2+BF2=EF2+CF2=EC2,EC2=AC2+AE2=2AC2,即可得出答案.
(1)∵AB=AC,△ACE是等腰直角三角形,
∴AB=AE,
∴∠ABE=∠AEB,
又∵∠BAC=50°,∠EAC=90°,
∴∠BAE=50°+90°=140°,
∴∠AEB=(180°-140°)÷2=20°;
(2)∵AB=AC,D是BC的中点,
∴∠BAF=∠CAF.
在△BAF和△CAF中
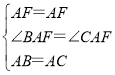 ,
,
∴△BAF≌△CAF(SAS),
∴∠ABF=∠ACF,
∵∠ABE=∠AEB,
∴∠AEB=∠ACF;
(3)∵△BAF≌△CAF,
∴BF=CF,
∵∠AEB=∠ACF,∠AGE=∠FGC,
∴∠CFG=∠EAG=90°,
∴EF2+BF2=EF2+CF2=EC2,
∵△ACE是等腰直角三角形,
∴∠CAE=90°,AC=AE,
∴EC2=AC2+AE2=2AC2,
即EF2+BF2=2AC2.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目