��Ŀ����
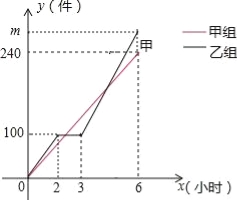
����Ŀ���ס������鹤��ͬʱ�ӹ�ij������������ڹ�������һ��ͣ�������豸��֮������Ĺ���Ч����ԭ����1.2�����ס�������ӹ������������һ��װ�䣬ÿ200��װһ�䣬���װ���ʱ����Բ��ƣ�������Լӹ����������y��������ʱ��x��ʱ���ĺ���ͼ����ͼ������˵��������ǣ� ��
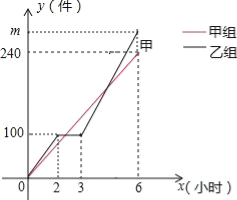
A������ӹ��������y��ʱ��x�Ĺ�ϵʽΪy��=40x
B������ӹ��������m=280
C������![]() Сʱǡ��װ����1��
Сʱǡ��װ����1��
D������![]() Сʱǡ��װ����2��
Сʱǡ��װ����2��
���𰸡�D
��������
�����������ͼ��ԭ�㼰��6��240����
�����ʽΪy=kx����6k=240�����k=40��
������ӹ��������y��ʱ��x�Ĺ�ϵʽΪy��=40x��0��x��6�����ʣ�A����ȷ��
����2Сʱ�ӹ�100����
���ҵļӹ��ٶ���ÿСʱ50����
����������豸������Ĺ���Ч����ԭ����1.2����
������Ĺ���Ч����ÿСʱ�ӹ���50��1.2=60����
��m=100+60����6��3��=280���ʣ�B����ȷ��
��������豸������ӹ�������ĸ���y��ʱ��x�ĺ�����ϵʽΪ��y=100+60��x��3��=60x��80��
��0��x��2ʱ��40x+50x=200����ã�x=![]() ���������⣩��
���������⣩��
��2��x��3ʱ��100+40x=200����ã�x=![]() ���������⣩��
���������⣩��
������![]() Сʱǡ��װ����1�䣬�ʣ�C����ȷ��
Сʱǡ��װ����1�䣬�ʣ�C����ȷ��
����3��x��6ʱ��40x+��60x��80��=200��2��
���x=4.8���������⣩��
������4.8Сʱǡ��װ����2�䣬�ʣ�D������
��ѡ��D

����Ŀ����֪���κ���y=ax2+bx+c��a��0���������Ա���x�뺯��ֵy֮����������Ķ�Ӧ��ϵ��
x | ���� | 3 | 5 | 7 | ���� |
y | ���� | 3.5 | 3.5 | -2 | ���� |
��a+b+c=______��