题目内容
【题目】在△ABC中,点O是△ABC的内心,连接OB、OC,过点O作EF∥BC分别交AB、AC于点E、F,已知BC=a (a是常数),设△ABC的周长为y,△AEF的周长为x,在下列图象中,大致表示y与x之间的函数关系的是( )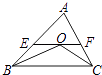
A.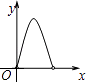
B.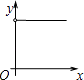
C.
D.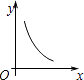
【答案】C
【解析】解:如图,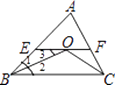
∵点O是△ABC的内心,
∴∠1=∠2,
又∵EF∥BC,
∴∠3=∠2,
∴∠1=∠3,
∴EO=EB,
同理可得FO=FC,
∵x=AE+EO+FO+AF,
y=AE+BE+AF+FC+BC,
∴y=x+a,(x>0),
即y是x的一次函数,
所以C选项正确.
故选C.
由于点O是△ABC的内心,根据内心的性质得到OB、OC分别平分∠ABC、∠ACB,又EF∥BC,可得到∠1=∠3,则EO=EB,同理可得FO=FC,再根据周长的所以可得到y=x+a,(x>0),即它是一次函数,即可得到正确选项.

练习册系列答案
相关题目