题目内容
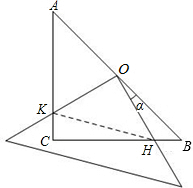 已知在△ABC中,∠ACB=90°,AC=BC=4,现将一块边长足够大的直角三角板的直角顶点置于AB的中点O,两直角边分别经过点B、C,然后将三角板绕点O按顺时针方向旋转一个角度α(0°<α<90°),旋转后,直角三角板的直角边分别与AC、BC相交于点K、H,四边形CHOK是旋转过程中三角板与△ABC的重叠部分(如图所示).那么,在上述旋转过程中:
已知在△ABC中,∠ACB=90°,AC=BC=4,现将一块边长足够大的直角三角板的直角顶点置于AB的中点O,两直角边分别经过点B、C,然后将三角板绕点O按顺时针方向旋转一个角度α(0°<α<90°),旋转后,直角三角板的直角边分别与AC、BC相交于点K、H,四边形CHOK是旋转过程中三角板与△ABC的重叠部分(如图所示).那么,在上述旋转过程中:(1)线段BH与CK具有怎样的数量关系?四边形CHOK的面积是否发生变化?证明你发现的结论;
(2)连接HK,设BH=x.
①当△CHK的面积为
| 3 | 2 |
②试问△OHK的面积是否存在最小值,若存在,求出此时x的值,若不存在,请说明理由.
分析:(1)连接OC,可以证得:△COK≌△BOH,根据S四边形CHOK=S△COK+S△COH=S△BOH+S△COH=S△COB=
S△ABC即可证得:四边形CHOK的面积始终保持不变;
(2)①BC=4,CH=4-x,三角形的面积公式可以得到:
CH•CK=
,即(4-x)x=3,从而求得x的值;
②设△OKH的面积为S,根据三角形的面积公式,即可得到关于x的函数关系式,然后根据函数的性质即可求解.
| 1 |
| 2 |
(2)①BC=4,CH=4-x,三角形的面积公式可以得到:
| 1 |
| 2 |
| 3 |
| 2 |
②设△OKH的面积为S,根据三角形的面积公式,即可得到关于x的函数关系式,然后根据函数的性质即可求解.
解答:解:(1)在旋转过程中,BH=CK,四边形CHOK的面积始终保持不变,其值为△ABC面积的一半.
理由如下:
连接OC
∵△ABC为等腰直角三角形,O为斜边AB的中点,CO⊥AB
∴∠OCK=∠B=45°,CO=OB,又∵∠COK与∠BOH均为旋转角,
∴∠COK=∠BOH=α
∴△COK≌△BOH
∴BH=CK,S四边形CHOK=S△COK+S△COH=S△BOH+S△COH=S△COB=
S△ABC=4.
(2)①由(1)知CK=BH=x,
∵BC=4,
∴CH=4-x,根据题意,得
CH•CK=
,即(4-x)x=3,
解这个方程得x1=1,x2=3,
此两根满足条件:0<x<4
所以当△CKH的面积为
时,x的取值是1或3;
②设△OKH的面积为S,由(1)知四边形CHOK的面积为4,于是得关系式:
S=4-S△CKH=4-
x(4-x)=
(x2-4x)+4
=
(x-2)2+2
当x=2时,函数S有最小值2,
∵x=2时,满足条件0<x<4,
∴△OKH的面积存在最小值,此时x的值是2.
理由如下:
连接OC
∵△ABC为等腰直角三角形,O为斜边AB的中点,CO⊥AB
∴∠OCK=∠B=45°,CO=OB,又∵∠COK与∠BOH均为旋转角,
∴∠COK=∠BOH=α
∴△COK≌△BOH
∴BH=CK,S四边形CHOK=S△COK+S△COH=S△BOH+S△COH=S△COB=
| 1 |
| 2 |
(2)①由(1)知CK=BH=x,
∵BC=4,
∴CH=4-x,根据题意,得
| 1 |
| 2 |
| 3 |
| 2 |
解这个方程得x1=1,x2=3,
此两根满足条件:0<x<4
所以当△CKH的面积为
| 3 |
| 2 |
②设△OKH的面积为S,由(1)知四边形CHOK的面积为4,于是得关系式:
S=4-S△CKH=4-
| 1 |
| 2 |
| 1 |
| 2 |
=
| 1 |
| 2 |
当x=2时,函数S有最小值2,
∵x=2时,满足条件0<x<4,
∴△OKH的面积存在最小值,此时x的值是2.
点评:本题考查了三角形全等的判定与性质,以及二次函数的性质,正确列出函数解析式是解题的关键.

练习册系列答案
 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
 22、如图,已知在△ABC中,∠A=(2x+10)°,∠B=(3x)°,∠ACD是△ABC的一个外角,且∠ACD=(6x-10)°,求∠A的度数.
22、如图,已知在△ABC中,∠A=(2x+10)°,∠B=(3x)°,∠ACD是△ABC的一个外角,且∠ACD=(6x-10)°,求∠A的度数.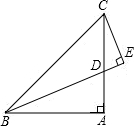 如图,已知在△ABC中,∠BAC为直角,AB=AC,D为AC上一点,CE⊥BD于E.若BD平分∠ABC.
如图,已知在△ABC中,∠BAC为直角,AB=AC,D为AC上一点,CE⊥BD于E.若BD平分∠ABC. 如图,已知在△ABC中,∠B与∠C的平分线交于点P.
如图,已知在△ABC中,∠B与∠C的平分线交于点P.