题目内容
若方程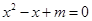
有两个不相等的实数根，则
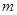的取值范围是 ▲ ．
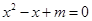有两个不相等的实数根，则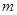的取值范围是 ▲ ．
本题是对根的判别式的应用，因为方程x2-x+m=0有两个不相等的实数根，所以△=b2-4ac＞0，然后列出关于m的不等式求解即可．
解：∵方程x2-x+m=0有两个不相等的实数根，
∴△=b2-4ac＞0，
即(-1)2-4×1×m＞0，
解这个不等式得：m＜
．
故本题答案为：．
总结：一元二次方程根的情况与判别式△的关系：
（1）△＞0?方程有两个不相等的实数根；
（2）△=0?方程有两个相等的实数根；
（3）△＜0?方程没有实数根．
解：∵方程x2-x+m=0有两个不相等的实数根，
∴△=b2-4ac＞0，
即(-1)2-4×1×m＞0，
解这个不等式得：m＜
．故本题答案为：
．总结：一元二次方程根的情况与判别式△的关系：
（1）△＞0?方程有两个不相等的实数根；
（2）△=0?方程有两个相等的实数根；
（3）△＜0?方程没有实数根．
练习册系列答案
智能训练练测考系列答案
相关题目
有两个同号的实数根，m的取值范围是 （ ）
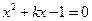，是否存在实数k，使得方程有两根分别为
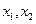且满足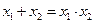
，若有求出k的值；若没有，请说明理由。
，则a的取值范围是 （ ）．
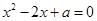有两个相等的实数根，那么a=________.
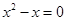时，只得出一个根x=1,则被漏掉的一个根是（ ）