题目内容
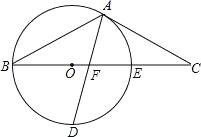
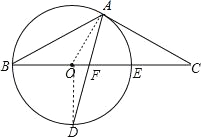
【题目】如图,以△ABC的BC边上一点O为圆心的圆,经过A,B两点,且与BC边交于点E,D为BE的下半圆弧的中点,连接AD交BC于F,AC=FC.
(1)求证:AC是⊙O的切线;
(2)已知圆的半径R=5,EF=3,求DF的长.
【答案】(1)证明见解析;(2)![]() .
.
【解析】
试题分析:(1)连结OA、OD,如图,根据垂径定理的推理,由D为BE的下半圆弧的中点得到OD⊥BE,则∠D+∠DFO=90°,再由AC=FC得到∠CAF=∠CFA,根据对顶角相等得∠CFA=∠DFO,所以∠CAF=∠DFO,加上∠OAD=∠ODF,则∠OAD+∠CAF=90°,于是根据切线的判定定理即可得到AC是⊙O的切线;
(2)由于圆的半径R=5,EF=3,则OF=2,然后在Rt△ODF中利用勾股定理计算DF的长.
试题解析:(1)连结OA、OD,如图,
∵D为BE的下半圆弧的中点,
∴OD⊥BE,
∴∠D+∠DFO=90°,
∵AC=FC,
∴∠CAF=∠CFA,
∵∠CFA=∠DFO,
∴∠CAF=∠DFO,
而OA=OD,
∴∠OAD=∠ODF,
∴∠OAD+∠CAF=90°,即∠OAC=90°,
∴OA⊥AC,
∴AC是⊙O的切线;
(2)∵圆的半径R=5,EF=3,
∴OF=2,
在Rt△ODF中,∵OD=5,OF=2,
∴DF=![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目