题目内容
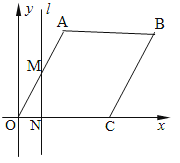
【题目】如图,在平面直角坐标系中,四边形OABC是菱形,点C的坐标为(4,0),∠AOC=60°,垂直于![]() 轴的直线l从
轴的直线l从![]() 轴出发,沿
轴出发,沿![]() 轴正方向以每秒1个单位长度的速度向右平移,设直线l与菱形OABC的两边分别交于点M,N(点M在点N的上方),若△OMN的面积为S,直线l的运动时间为t 秒。试问:S与t的函数关析式?
轴正方向以每秒1个单位长度的速度向右平移,设直线l与菱形OABC的两边分别交于点M,N(点M在点N的上方),若△OMN的面积为S,直线l的运动时间为t 秒。试问:S与t的函数关析式?
【答案】当0≤t≤2时,S=![]() t2;当2<t≤4时,S=4
t2;当2<t≤4时,S=4![]() t
t
【解析】
试题分析:沿x轴正方向运动与菱形OABC的两边相交有2种情况:分别列出0≤t≤2时和当2<t≤4时的函数解析式,进而利用函数的性质确定面积的最大值.
试题解析:直线l从y轴出发,沿x轴正方向运动与菱形OABC的两边相交有2种情况:
①0≤t≤2时,直线l与OA、OC两边相交
∵MN⊥OC,
∴ON=t
∴MN=ONtan60°=![]() t
t
∴S=![]() ONMN=
ONMN=![]() t2.
t2.
②当2<t≤4时,直线l与AB、OC两边相交
S=![]() ONMN=
ONMN=![]() ×t×2
×t×2![]() =
=![]() t.
t.
故当0≤t≤2时,S=![]() t2;当2<t≤4时,S=4
t2;当2<t≤4时,S=4![]() t
t

练习册系列答案
相关题目