题目内容
【题目】在△ABC中,AB=6,AC=8,BC=10,P为边BC上一动点,PE⊥AB于E,PF⊥AC于F,M为EF中点,则AM的最小值为_____.
【答案】2.4
【解析】
根据已知得当AP⊥BC时,AP最短,同样AM也最短,从而不难根据相似比求得其值.
连结AP,
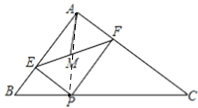
在△ABC中,AB=6,AC=8,BC=10,
∴∠BAC=90°,
∵PE⊥AB,PF⊥AC,
∴四边形AFPE是矩形,
∴EF=AP.
∵M是EF的中点,
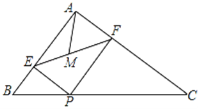
∴AM=![]() AP,
AP,
根据直线外一点到直线上任一点的距离,垂线段最短,即AP⊥BC时,AP最短,同样AM也最短,
∴当AP⊥BC时,△ABP∽△CAB,
∴AP:AC=AB:BC,
∴AP:8=6:10,
∴AP最短时,AP=4.8,
∴当AM最短时,AM=AP÷2=2.4.
故答案为2.4

练习册系列答案
相关题目
【题目】某班6名同学的身高(单位:cm)情况如下表:
同学 | A | B | C | D | E | F |
身高 | 165 | 166 | 171 | |||
身高与班级平均身高的差值 | -1 | +2 | -3 | +3 |
(1)完成表中空白的部分;
(2)他们的最高身高与最矮身高相差多少?
(3)他们6人的平均身高是多少?