题目内容
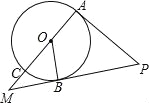
【题目】如图,AC是⊙O的直径,OB是⊙O的半径,PA切⊙O于点A,PB与AC的延长线交于点M,∠COB=∠APB.
(1)求证:PB是⊙O的切线;
(2)当OB=3,PA=6时,求MB,MC的长.
【答案】(1)证明参见解析;(2)MB=4,MC=2.
【解析】
试题分析:(1)证出OB垂直PM是解题的关键,根据切线的性质,可得∠MAP=90°,根据直角三角形的性质,可得∠P+M=90°,根据余角的性质,可得∠M+∠MOB=90°,根据直角三角形的判定,可得∠MOB=90°,根据切线的判定,可得答案;(2)根据相似三角形的判定与性质,可得△OBM∽△APM,于是有![]() =
=![]() =
=![]() ,根据解方程组,可得答案.
,根据解方程组,可得答案.
试题解析:(1)根据题意,∵PA切⊙O于点A,∴∠MAP=90°,∴∠P+∠M=90°.∵∠COB=∠APB,∴∠M+∠MOB=90°,∴∠MBO=90°,即OB⊥PB,∵PB经过直径的外端点,∴PB是⊙O的切线;(2)∵∠COB=∠APB,∠OBM=∠PAM,∴△OBM∽△APM,∴![]() =
=![]() =
=![]() ,
,![]() =
=![]() ①,
①,![]() =
=![]() ②,联立①②得
②,联立①②得![]() ,解得
,解得![]() ,所以当OB=3,PA=6时,MB=4,MC=2.
,所以当OB=3,PA=6时,MB=4,MC=2.

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
【题目】如图,已知抛物线P:y=ax2+bx+c(a≠0)与x轴交于A、B两点(点A在x轴的正半轴上),与y轴交于点C,矩形DEFG的一条边DE在线段AB上,顶点F、G分别在线段BC、AC上,抛物线P上部分点的横坐标对应的纵坐标如下:
x | … | ﹣3 | ﹣2 | 1 | 2 | … |
y | … |
| ﹣4 |
| 0 | … |
(1)求A、B、C三点的坐标;
(2)若点D的坐标为(m,0),矩形DEFG的面积为S,求S与m的函数关系,并指出m的取值范围;
(3)当矩形DEFG的面积S取最大值时,连接DF并延长至点M,使FM=kDF,若点M不在抛物线P上,求k的取值范围.