题目内容
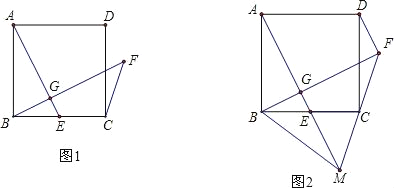
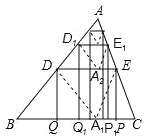
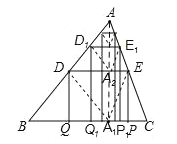
【题目】如图,将△ABC沿着过AB中点D的直线折叠,使点A落在BC边上的A1处,折痕与AC边交于点E,分别过点D、E作BC的垂线,垂足为Q、P,称为第1次操作,记四边形DEPQ的面积为S1;还原纸片后,再将△ADE沿着过AD中点D1的直线折叠,使点A落在DE边上的A2处,折痕与AC边交于点E1,分别过点D1、E1作BC的垂线,垂足为Q1、P1,称为第2次操作,记四边形D1E1P1Q1的面积为S2;按上述方法不断操作下去…,若△ABC的面积为1,则Sn的值为( )
A.![]() B.
B. ![]() C.
C. ![]() D.
D.![]()
【答案】B
【解析】
试题分析:连接AA1,
由折叠的性质可得:AA1⊥DE,DA=DA1,
又∵D是AB中点,
∴DA=DB,
∴DB=DA1,
∴∠BA1D=∠B,
∴∠ADA1=2∠B,
又∵∠ADA1=2∠ADE,
∴∠ADE=∠B,
∴DE∥BC,
∴AA1⊥BC,
∴四边形DEPQ的面积为S1=DQ×DE=(AA1﹣AA2)×DE=(1﹣![]() )AA1×
)AA1×![]() BC=(1﹣
BC=(1﹣![]() )×
)×![]() ×2S△ABC=(1﹣
×2S△ABC=(1﹣![]() )×
)×![]() ×2
×2
同理,四边形D1E1P1Q1的面积为S2=D1Q1×D1E1=(AA1﹣AA3)×D1E1=(1﹣![]() )×
)×![]() ×2
×2
四边形D2E2P2Q2的面积为S3=D2Q2×D2E2=(AA1﹣AA4)×D2E2=(1﹣![]() )×
)×![]() ×2
×2
…
∴Sn的值为:[1﹣(![]() )n]×(
)n]×(![]() )n×2=
)n×2=![]()
故选(B)

练习册系列答案
相关题目