题目内容
【题目】如图1,正方形ABCD中,E为BC上一点,过B作BG⊥AE于G,延长BG至点F使∠CFB=45°
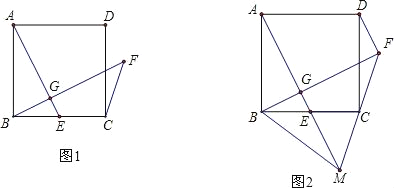
(1)求证:AG=FG;
(2)如图2延长FC、AE交于点M,连接DF、BM,若C为FM中点,BM=10,求FD的长.
【答案】(1)证明见解析;(2)2![]() .
.
【解析】
试题分析:(1)过C点作CH⊥BF于H点,根据已知条件可证明△AGB≌△BHC,所以AG=BH,BG=CH,又因为BH=BG+GH,所以可得BH=HF+GH=FG,进而证明AG=FG;
(2)过D作DQ⊥MF交MF延长线于Q,根据全等三角形的性质和等腰三角形的性质即可求出FD的长.
试题解析:(1)过C点作CH⊥BF于H点,
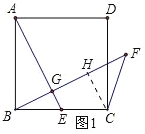
∵∠CFB=45°
∴CH=HF,
∵∠ABG+∠BAG=90°,∠FBE+∠ABG=90°
∴∠BAG=∠FBE,
∵AG⊥BF,CH⊥BF,
∴∠AGB=∠BHC=90°,
在△AGB和△BHC中,
∵∠AGB=∠BHC,∠BAG=∠HBC,AB=BC,
∴△AGB≌△BHC,
∴AG=BH,BG=CH,
∵BH=BG+GH,
∴BH=HF+GH=FG,
∴AG=FG;
(2)∵CH⊥GF,
∴CH∥GM,
∵C为FM的中点,
∴CH=![]() GM,
GM,
∴BG=![]() GM,
GM,
∵BM=10,
∴BG=2![]() ,GM=4
,GM=4![]() ,
,
∴AG=4![]() ,AB=10,
,AB=10,
∴HF=2![]() ,
,
∴CF=2![]() ×
×![]() =2
=2![]() ,
,
∴CM=2![]() ,
,
过B点作BK⊥CM于K,
∵CK=![]() CM=
CM=![]() CF=
CF=![]() ,
,
∴BK=3![]() ,
,
过D作DQ⊥MF交MF延长线于Q,
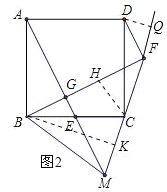
∴△BKC≌△CQD
∴CQ=BK=3![]() ,
,
DQ=CK=![]() ,
,
∴QF=3![]() -2
-2![]() =
=![]() ,
,
∴DF=![]() =2
=2![]() .
.

 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案 应用题作业本系列答案
应用题作业本系列答案【题目】点P为直线l外一点,点A,B,C为直线l上三点,PA=4 cm,PB=5 cm,PC=2 cm,则点P到直线l的距离为( )
A. 5 cm B. 4 cm C. 2 cm D. 不大于2 cm
【题目】某公司欲招聘一名管理人员,对甲、乙两名竞聘者进行了两项测试,各项测试成绩如下表:
测试项目 | 测试成绩(分) | |
甲 | 乙 | |
笔试 | 75 | 84 |
面试 | 88 | 72 |
公司将笔试、面试两项测试成绩分别以60%、40%记入个人最后成绩,并根据成绩择优录用,你认为谁将被录用?(要求写出计算过程)