题目内容
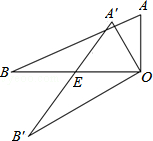
如图,在Rt△ABC中,∠C=90°,AC= ,BC=1,D在AC上,将△ADB沿直线BD翻折后,点A落在点E处,如果AD⊥ED,那么△ABE的面积是
,BC=1,D在AC上,将△ADB沿直线BD翻折后,点A落在点E处,如果AD⊥ED,那么△ABE的面积是

 ,BC=1,D在AC上,将△ADB沿直线BD翻折后,点A落在点E处,如果AD⊥ED,那么△ABE的面积是
,BC=1,D在AC上,将△ADB沿直线BD翻折后,点A落在点E处,如果AD⊥ED,那么△ABE的面积是
| A.1 | B. | C. | D. |
A
试题分析:∵∠C=90°,AC=
 ,BC=1,∴根据勾股定理得AB=2。∴∠BAC=30°。
,BC=1,∴根据勾股定理得AB=2。∴∠BAC=30°。∵△ADB沿直线BD翻折后,点A落在点E处,
∴BE=BA=2,∠BED=∠BAD=30°,DA=DE。
∵AD⊥ED,∴BC∥DE。∴∠CBF=∠BED=30°。
在Rt△BCF中,
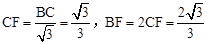 ,∴EF=2﹣
,∴EF=2﹣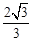 。
。在Rt△DEF中,FD=
 EF=1﹣
EF=1﹣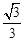 ,ED=
,ED= FD=
FD= ﹣1。
﹣1。∴S△ABE=S△ABD+S△BED+S△ADE=2S△ABD+S△ADE=2×
 BC•AD+
BC•AD+ AD•ED
AD•ED=2×
 ×1×(
×1×( ﹣1)+
﹣1)+ ×(
×( ﹣1)(
﹣1)( ﹣1)=1。
﹣1)=1。故选A。

练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案
相关题目